Question
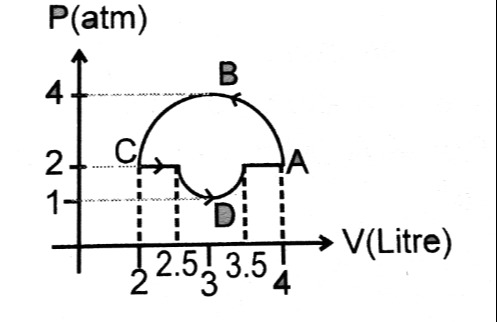
Question: P(atm) V(Litre)...
P(atm)
V(Litre)
Answer
The net work done during the cycle is approximately 1+π L atm or 419.6 J, assuming the curved path A-B-C is a semi-ellipse.
Explanation
Solution
The problem presents a P-V diagram of a thermodynamic cycle. To find the net work done, we calculate the area enclosed by the cycle.
-
Work Done in Straight Line Segments:
- C -> D: WC→D=1.5 L atm
- D -> A: WD→A=1.5 L atm
-
Area Under the Lower Path (C-D-A):
- Total area = 1.5+1.5=3 L atm
-
Approximation of the Curved Path (A-B-C):
- Assuming the curve A-B-C is a semi-ellipse with center at (3, 2), semi-major axis of 2 (along the P-axis), and semi-minor axis of 1 (along the V-axis).
- The area enclosed by a semi-ellipse is A=21πab=21π(1)(2)=π.
-
Net Work Calculation:
- The area under the semi-ellipse (A-B-C) from V=2 to V=4 is then calculated as: ∫24PupperdV=4+π.
- Wcycle=∫24PupperdV−3.
- Wcycle=(4+π)−3=1+π≈4.14 L atm.
-
Conversion to Joules:
- 1 L atm=101.325 J
- Wcycle=(1+π)×101.325≈419.6 J
Thus, the net work done during the cycle is approximately 1+π L atm or 419.6 J, assuming the curved path A-B-C is a semi-ellipse. The positive value indicates that the cycle is clockwise, and the system performs work on the surroundings.
