Question

Passengers in the jet transport A flying east at a speed of $800km/h$ observe a second jet plane B that passes under the transport in horizontal flight. Although the nose of B is pointed in the $45{}^\circ$ north east direction, plane B appears to the passengers in A to be moving away from the transport at the $60{}^\circ$ angle as shown. The true velocity of B is :

& A)586km/h \\\ & B)400\sqrt{2}km/h \\\ & C)717km/h \\\ & D)400km/h \\\ \end{aligned}$$

Answer 1

The magnitude and direction of velocity of plane A and direction of plane B are given. From this relative velocity of plane B with respect to A can be determined. Using these three velocities a vector diagram can be drawn. Using Lami’s theorem, we can equate these velocities and thereby we can determine the velocity of plane B.
Formula used:
${{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}$
$\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B/A}}}{\sin 45}$

Complete step by step solution:
The relative velocity of B with respect to A is given by,
${{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}$
Where,
${{\vec{v}}_{A}}$is the velocity of Plane A
${{\vec{v}}_{B}}$is the velocity of Plane B
The vectors ${{\vec{v}}_{B/A}}$, ${{\vec{v}}_{B}}$and ${{\vec{v}}_{A}}$ make a triangle.

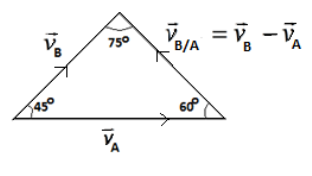
Given,
Velocity of plane A,${{v}_{A}}=800\hat{i}$
According to Lami’s theorem,
$\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B/A}}}{\sin 45}$
We have,
${{\vec{v}}_{B/A}}={{\vec{v}}_{B}}-{{\vec{v}}_{A}}$
Substitute it in above equation , we get,
$\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}=\dfrac{{{{\vec{v}}}_{B}}-{{{\vec{v}}}_{A}}}{\sin 45}$
Then,
$\dfrac{{{{\vec{v}}}_{A}}}{\sin 75}=\dfrac{{{{\vec{v}}}_{B}}}{\sin 60}$
Substitute the value of ${{\vec{v}}_{A}}$in the above equation
${{\vec{v}}_{B}}=800\times \dfrac{\sin 60}{\sin 75}=717km/h$

Therefore, the answer is option C.

Note:
Lami’s theorem relates the magnitudes of three concurrent, non-collinear and coplanar which keeps an object in static equilibrium, with the angles directly opposite to the corresponding vectors. According to the theorem,
$\dfrac{A}{\sin \alpha }=\dfrac{B}{\sin \beta }=\dfrac{C}{\sin \gamma }$
Where A, B and C are the magnitudes of the three concurrent coplanar and noncollinear vectors ${{\vec{v}}_{A}}$, ${{\vec{v}}_{B}}$ and ${{\vec{v}}_{C}}$and α, β and γ are the angles directly opposite to the vectors.