Question
Question: The rate constant of the reaction is $\bigcirc$ 10$^{-5}$mmHg$^{-2}$ s$^{-1}$ $\bigcirc$ 10$^{-6}$...
The rate constant of the reaction is
◯ 10−5mmHg−2 s−1
◯ 10−6mmHg−2 s−1
◯ 10−7mmHg−2 s−1
◯ 10−8mmHg−2 s−1
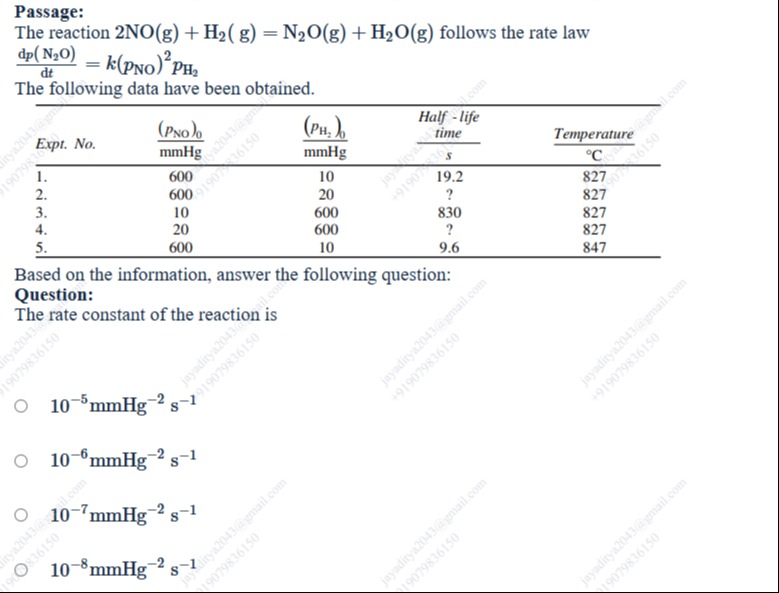
10−5mmHg−2 s−1
10−6mmHg−2 s−1
10−7mmHg−2 s−1
10−8mmHg−2 s−1
10−7mmHg−2 s−1
Solution
The rate law is given as dtdp(N2O)=k(pNO)2pH2.
From Experiment 1, (pNO)0=600 mmHg, (pH2)0=10 mmHg, t1/2=19.2 s at 827 °C. Since (pNO)0≫(pH2)0, the reaction is pseudo-first order with respect to H2, with effective rate constant k′=k(pNO)02. The half-life is t1/2=k′ln2. So, 19.2=k(600)2ln2, which gives k=19.2×6002ln2≈1.00×10−7 mmHg−2 s−1.
From Experiment 3, (pNO)0=10 mmHg, (pH2)0=600 mmHg, t1/2=830 s at 827 °C. Since (pH2)0≫(pNO)0, the reaction is pseudo-second order with respect to NO, with effective rate constant for consumption of NO as 2k′′=2k(pH2)0. The half-life for a second-order reaction is t1/2=keff(pNO)01. Here, keff is the rate constant for the decrease in concentration of NO in the second-order rate law −dtdpNO=keff(pNO)2. From the given rate law, −dtdpNO=2k(pNO)2pH2. With pseudo-second order approximation, −dtdpNO=2k(pNO)2(pH2)0. So keff=2k(pH2)0. The half-life is t1/2=2k(pH2)0(pNO)01. So, 830=2k×600×101, which gives k=830×2×600×101≈1.00×10−7 mmHg−2 s−1.
Both experiments give a consistent value of k around 10−7 mmHg−2 s−1 at 827 °C.
