Solveeit Logo
Login

Question

Question: Particle released at origin with \(v = {v_0}i\) and \(E = {E_0}j\) and \(B = {B_0}j\). So what would...

Particle released at origin with v=v0iv = {v_0}i and E=E0jE = {E_0}j and B=B0jB = {B_0}j. So what would the path be like?

Explanation

Solution

A particle moving in a magnetic field will experience force. So in this question we will find the direction of force acting on the particle and using this we will find the direction in which the particle will move. Based on this observation we will find the path of the particle.

Complete step by step answer:
We can see that as the particle moves in the magnetic field B=B0jB = {B_0}j a force will act on the particle. This force will be centripetal force which is given by following formula,
FC=mv2r{F_C} = \dfrac{{m{v^2}}}{r}
Where,
M is mass of the particle
V is the velocity of the particle
R is the radius of its path
If the charge on the particle is q then the magnetic field will apply a force which will be equal to F=qvBF = qvB.
Since both the forces are applied by the magnetic field so we can equate these forces and we get following equation,
mv2r=qvB\dfrac{{m{v^2}}}{r} = qvB -----(1)
From this equation we will find the radius of curvature
r=mv2qvBr = \dfrac{{m{v^2}}}{{qvB}}
r=mvqBr = \dfrac{{mv}}{{qB}}
There will be two components of velocity vperp=vsin⁡θ{v_{perp}} = v\sin \theta and vpara=vcos⁡θ{v_{para}} = v\cos \theta
θ\theta is the angle between v and B

As we can see in the question that the angle between v and B is 90∘{90^\circ }. So only the perpendicular component will remain and the parallel component will become zero. So the particle will move in a circular path only.

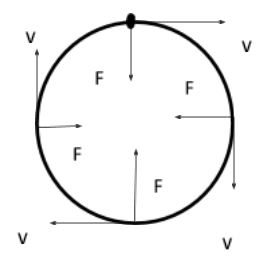
Path of particle moving in magnetic field B=B0jB = {B_0}j with velocity v=v0iv = {v_0}i
Result- From above explanation, we can see that the path of particle moving with v=v0iv = {v_0}i in E=E0jE = {E_0}j and B=B0jB = {B_0}j is circular.

Note: In such a type of question we have to pay attention to the motion of the particle. If the particle is at rest then the path of the particle will be a straight line. If the angle between velocity and magnetic field is 90∘{90^\circ } then the path will be circular. If the angle between velocity and magnetic field is θ\theta then the path of the particle will be helical.