Question

Let a and b be real numbers greater than 1 for which there exists a positive real number c, different from 1, such that $2(log_a c + log_b c) = 9log_{ab}c$, then the possible value of $log_a b$.

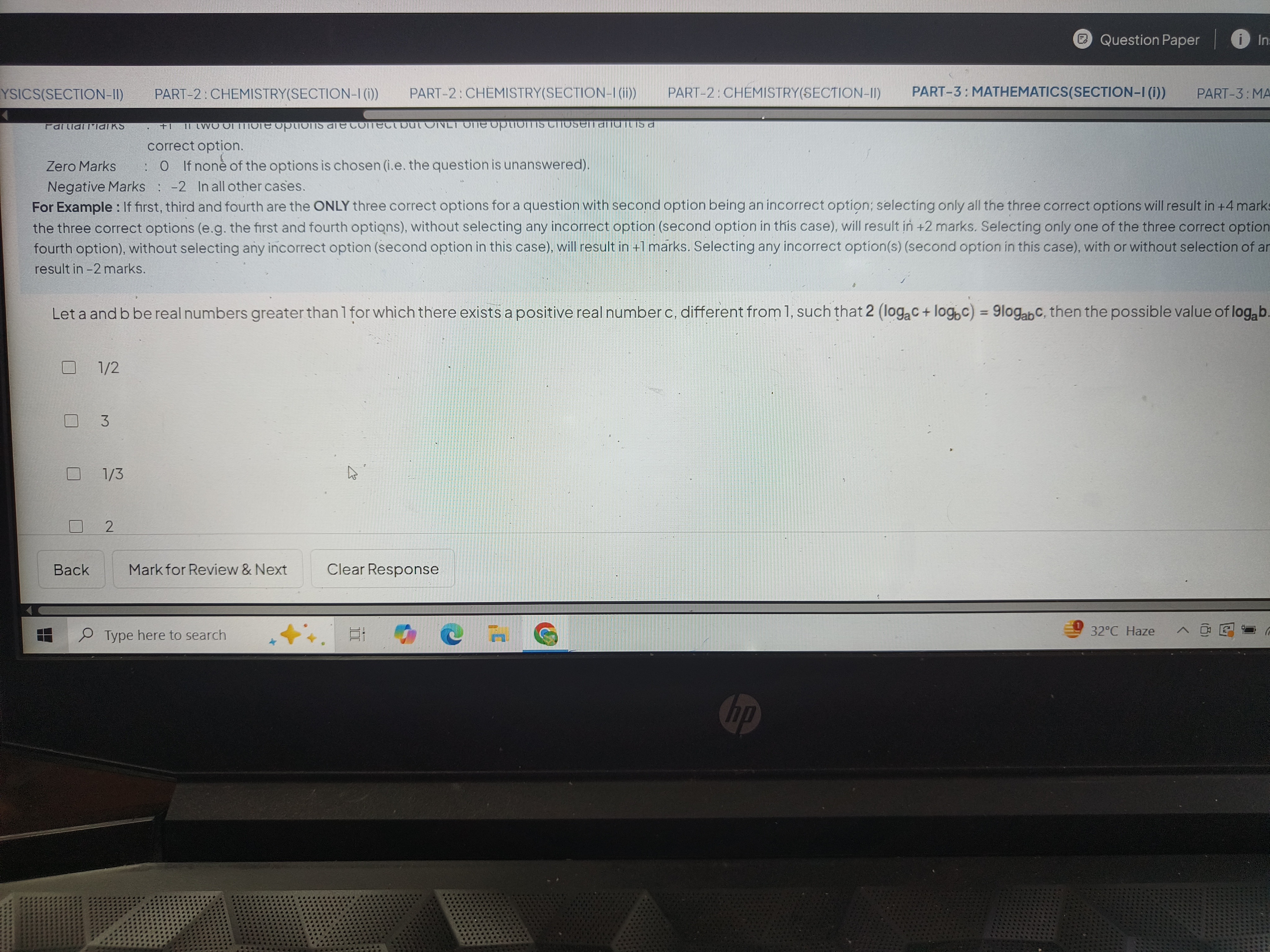
• A. 1/2
• B. 3
• C. 1/3
• D. 2

Answer 1

Answer: (A), (D)

1/2, 2

Answer 2

The given equation is $2(\log_a c + \log_b c) = 9\log_{ab}c$. We are given that $a, b > 1$ and $c > 0, c \neq 1$. We need to find the possible value(s) of $\log_a b$.

1. Use the change of base formula for logarithms: $\log_x y = \frac{1}{\log_y x}$. Applying this to all terms with base $c$: $\log_a c = \frac{1}{\log_c a}$ $\log_b c = \frac{1}{\log_c b}$ $\log_{ab} c = \frac{1}{\log_c (ab)}$

2. Substitute these expressions into the given equation: $2\left(\frac{1}{\log_c a} + \frac{1}{\log_c b}\right) = \frac{9}{\log_c (ab)}$

3. Simplify the left side of the equation: $2\left(\frac{\log_c b + \log_c a}{\log_c a \cdot \log_c b}\right) = \frac{9}{\log_c (ab)}$

4. Use the logarithm property $\log_x M + \log_x N = \log_x (MN)$. So, $\log_c a + \log_c b = \log_c (ab)$. Substitute this into the equation: $2\left(\frac{\log_c (ab)}{\log_c a \cdot \log_c b}\right) = \frac{9}{\log_c (ab)}$

5. Let $x = \log_c a$ and $y = \log_c b$. The equation becomes: $2\left(\frac{x+y}{xy}\right) = \frac{9}{x+y}$

6. Cross-multiply and rearrange the terms: $2(x+y)^2 = 9xy$ $2x^2 - 5xy + 2y^2 = 0$

7. We want to find $\log_a b = \frac{\log_c b}{\log_c a} = \frac{y}{x}$. Divide the entire equation by $x^2$: $2 - 5\left(\frac{y}{x}\right) + 2\left(\frac{y}{x}\right)^2 = 0$

8. Let $k = \frac{y}{x} = \log_a b$. The equation becomes: $2k^2 - 5k + 2 = 0$

9. Solve the quadratic equation for $k$: $(2k-1)(k-2) = 0$ This gives two possible values for $k$: $k = \frac{1}{2}$ and $k = 2$.

Thus, the possible values of $\log_a b$ are $1/2$ and $2$.