Question
Question: Solution set of the inequality $\sqrt{x^2-x-6} < 2x-3$ is...
Solution set of the inequality x2−x−6<2x−3 is
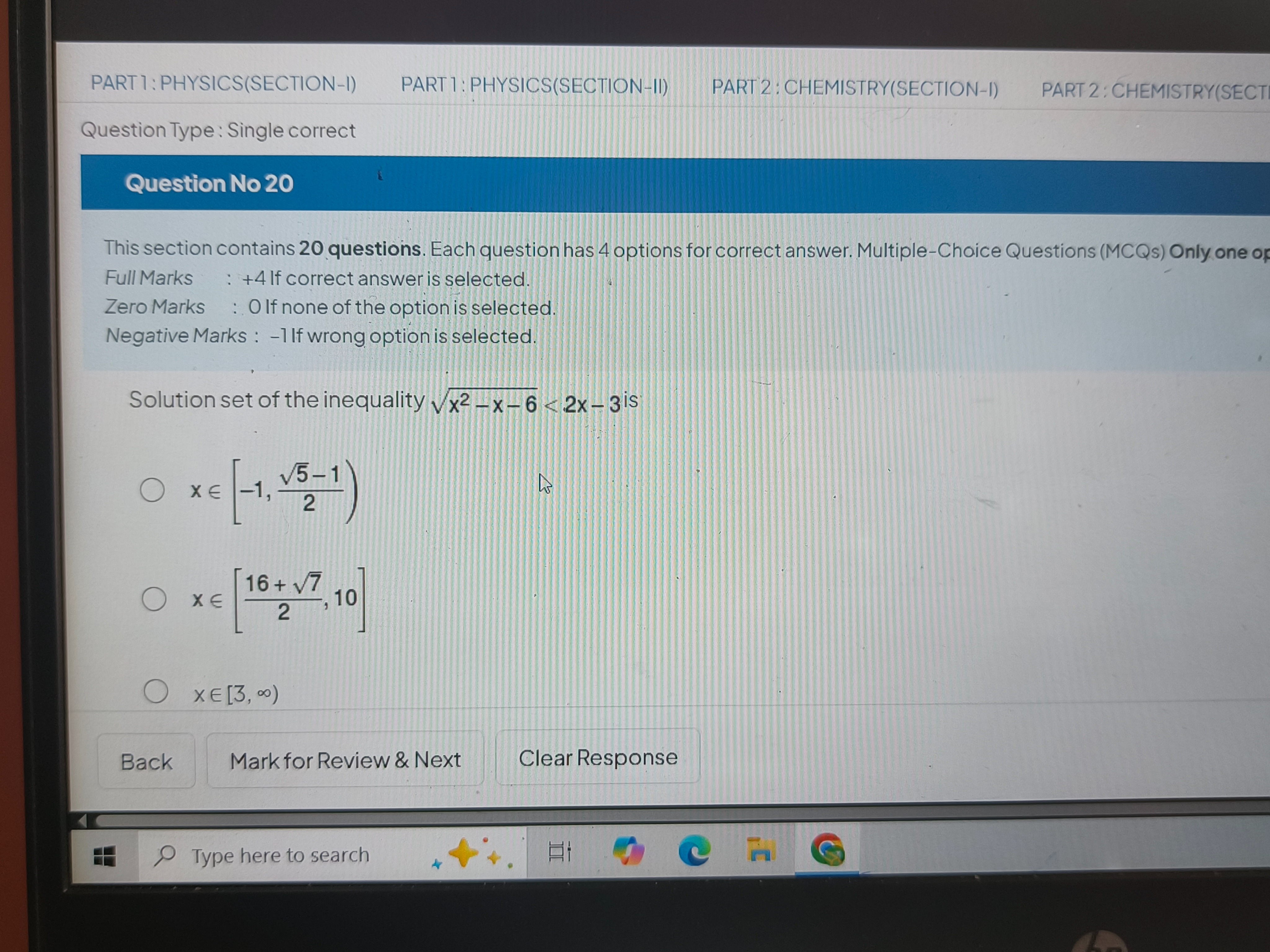
x∈[−1,25−1)
x∈[216+7,10]
x∈[3,∞)
x∈[3,∞)
Solution
To solve the inequality x2−x−6<2x−3, we need to consider three main conditions:
1. Domain of the square root:
For x2−x−6 to be defined in real numbers, the expression under the square root must be non-negative:
x2−x−6≥0
Factor the quadratic: (x−3)(x+2)≥0
The roots are x=3 and x=−2.
This inequality holds when x≤−2 or x≥3.
So, x∈(−∞,−2]∪[3,∞). (Condition 1)
2. Right Hand Side (RHS) must be positive:
For the inequality A<B to have a solution, B must be positive, since the square root of a real number is always non-negative.
2x−3>0
2x>3
x>23 (Condition 2)
3. Squaring both sides:
Since both sides of the inequality are non-negative (from Condition 2, 2x−3>0, and x2−x−6≥0), we can square both sides without changing the direction of the inequality:
(x2−x−6)2<(2x−3)2
x2−x−6<4x2−12x+9
Rearrange the terms to form a quadratic inequality:
0<4x2−x2−12x+x+9+6
0<3x2−11x+15
3x2−11x+15>0 (Condition 3)
To analyze Condition 3, let's find the discriminant (Δ) of the quadratic 3x2−11x+15:
Δ=b2−4ac=(−11)2−4(3)(15)
Δ=121−180
Δ=−59
Since the discriminant is negative (Δ<0) and the leading coefficient is positive (a=3>0), the quadratic 3x2−11x+15 is always positive for all real values of x.
So, Condition 3 is true for all x∈R.
4. Combine all conditions:
We need to find the intersection of Condition 1, Condition 2, and Condition 3.
Condition 1: x∈(−∞,−2]∪[3,∞)
Condition 2: x∈(23,∞)
Condition 3: x∈R
Let's find the intersection of Condition 1 and Condition 2:
The interval (−∞,−2] does not overlap with (23,∞) because −2<23.
The interval [3,∞) overlaps with (23,∞). Since 3>23, the intersection of [3,∞) and (23,∞) is [3,∞).
Since Condition 3 is true for all real x, it does not further restrict the solution set.
Therefore, the solution set for the inequality is x∈[3,∞).
