Question
Question: Part AC and DC of a conductor are parallel to z-axis and x-axis respectively as shown in figure. The...
Part AC and DC of a conductor are parallel to z-axis and x-axis respectively as shown in figure. The magnitude of magnetic field at point O has magnitude
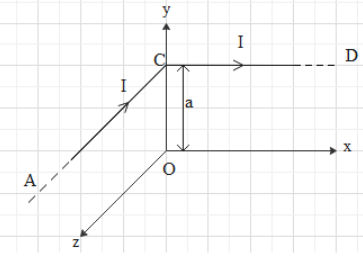
Solution
We have to find the magnitude of the magnetic field at point O for the given diagram. Now there are two conductors in which one is parallel to the z-axis whereas the other is parallel to x-axis. So we can find the magnetic field at O along the z-axis and x-axis with the help of Ampere’s law.
Formula used:
B=4πrμ0I
Complete answer:
From the given diagram we can see that there is a common point at C which is distanced ‘a’ from the point O and lying on the y-axis. Also the part AC and CD are perpendicular to the y-axis as well as AC is also perpendicular to CD.
Now according to Ampere’s law (for magnetic field), magnetic field of the conductor is given by
B=4πrμ0I
Where I is the current flowing through the conductor, r is the radius of the conductor and μ0is the permeability of the conductor.
If we consider the part AC which is lying parallel to z-axis and distance of it from Point O is a then the magnetic field at point O along the z-axis will be given as
Bz=4πaμ0Ik∧
Similarly for the part of conductor CD parallel to x-axis, the magnetic field at point O due to it, will be
Bx=4πaμ0Ii∧
Now we have asked the magnetic of the magnetic field at point O, which will be given as
