Question

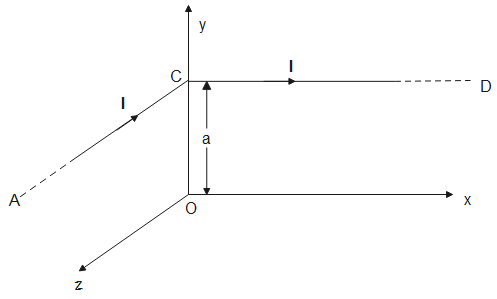
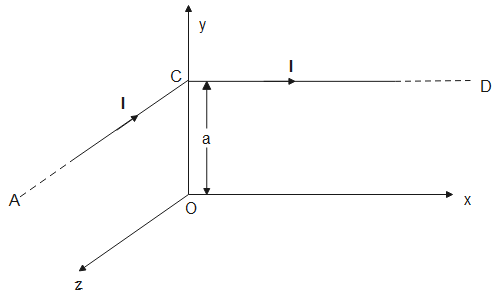
Part AC and CD of conductor are parallel to z-axis and x-axis respectively as shown in figure. What is the magnitude of the magnetic field at point O?

Answer 1

Magnetic field is a vector quantity. We have to find magnetic field at point O. Use relation of total magnetic field due to straight current carrying conductor and find magnetic field at O due to both the conductors AC and CD. Add the magnetic field due to both the conductors and then find the magnitude.
Formula used: Magnetic field due to a straight conductor, $\mathbf{B}=\dfrac{{{\mu }_{0}}I}{4\pi r}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})$

Complete answer:
From the diagram given, we can note that the distance of point O from the common point C of both the wires is the perpendicular distance from both wires.

According to Ampere’s law, magnetic field due to a straight conductor is given by
$\mathbf{B}=\dfrac{{{\mu }_{0}}I}{4\pi r}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})$
Where $I$ is the current flowing through the conductor, ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are the angles between the line joining the end of wire to the point where magnetic field is being measured and the normal from that point to the conductor. $r$ is the length of the normal.
Since, conductors given in the diagram are of infinite length and magnetic field is to be measured at a point perpendicular to its one end. Therefore, ${{\theta }_{1}}={{0}^{{}^\circ }}$and ${{\theta }_{2}}={{90}^{{}^\circ }}$. Substituting this our relation becomes
$\mathbf{B}=\dfrac{{{\mu }_{0}}I}{4\pi r}$
Now, magnetic field due to wire AC is ($r=a$)
${{\mathbf{B}}_{AC}}=\dfrac{{{\mu }_{0}}I}{4\pi a}(-\hat{i})$
Similarly, magnetic field due to wire CD is ($r=a$)
${{\mathbf{B}}_{CD}}=\dfrac{{{\mu }_{0}}I}{4\pi a}(-\hat{k})$
The direction of both these magnetic fields is perpendicular which can be found using right hand thumb rule.
Thus, magnitude of magnetic field at O due to conductors’ AC and CD is
$\left| {{\mathbf{B}}_{O}} \right|=\sqrt{B_{CD}^{2}+B_{AC}^{2}}=\dfrac{\sqrt{2}{{\mu }_{0}}I}{4\pi a}$

Note:
Magnetic field is a vector quantity so it can not be added directly as scalars. To find the magnitude of magnetic field due to two conductors, we must first add magnetic field due to both the conductors according to the law of vector addition and then find the magnitude of the resultant.