Question

If the triplets log a, log b, log c and (log a - log 2b), (log 2b - log 3c), (log 3c - log a) are in arithmetic progression then (Assume all logarithmic terms to be defined)

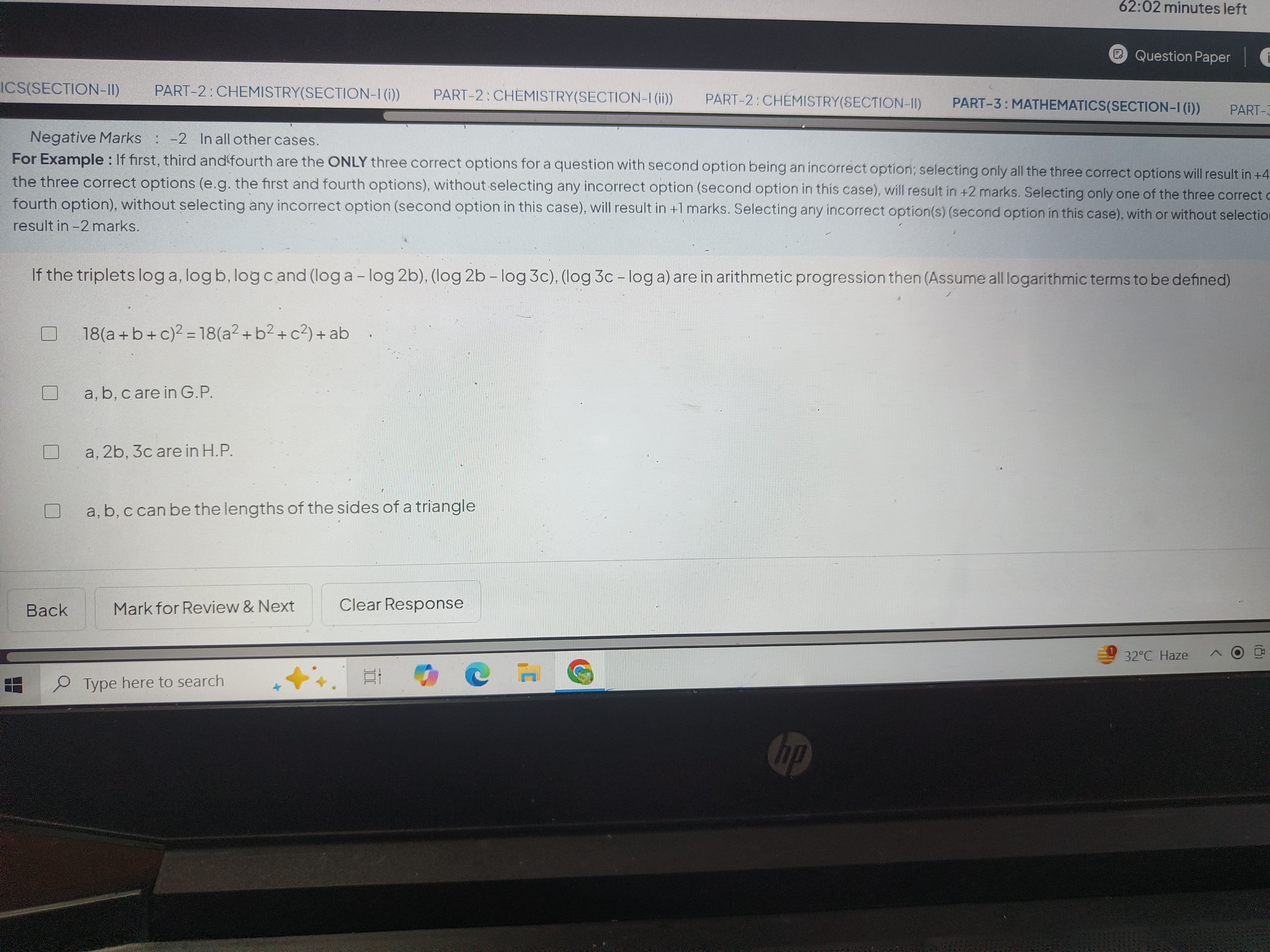
• A. 18(a + b + c)² = 18(a² + b²+c²) + ab
• B. a, b, c are in G.P.
• C. a, 2b, 3c are in H.P.
• D. a, b, c can be the lengths of the sides of a triangle

Answer 1

Answer: (B), (D)

a, b, c are in G.P., a, b, c can be the lengths of the sides of a triangle

Answer 2

The problem provides two triplets that are in arithmetic progression (AP) and asks us to determine which of the given options are true.

Step 1: Analyze the first triplet in AP

The first triplet is log a, log b, log c.

If x, y, z are in AP, then 2y = x + z.

Applying this property:

2 log b = log a + log c

Using logarithm properties (n log x = log x^n and log x + log y = log (xy)):

log (b^2) = log (ac)

Since the logarithmic function is one-to-one:

b^2 = ac

This is the defining property of a Geometric Progression (GP). Therefore, a, b, c are in G.P.

So, Option 2 is correct.

Step 2: Analyze the second triplet in AP

The second triplet is (log a - log 2b), (log 2b - log 3c), (log 3c - log a).

Let X = log a, Y = log 2b, Z = log 3c.

The triplet can be written as (X - Y), (Y - Z), (Z - X).

Applying the AP property 2 * (middle term) = (first term) + (last term):

2(Y - Z) = (X - Y) + (Z - X)

2Y - 2Z = X - Y + Z - X

2Y - 2Z = -Y + Z

Rearranging the terms to solve for Y and Z:

3Y = 3Z

Y = Z

Substitute back the original expressions for Y and Z:

log 2b = log 3c

Since the logarithmic function is one-to-one:

2b = 3c

Step 3: Establish relationships between a, b, and c

From Step 1, we have b^2 = ac.

From Step 2, we have 2b = 3c, which implies c = (2/3)b.

Substitute the expression for c into the equation from Step 1:

b^2 = a * (2/3)b

Since all logarithmic terms are defined, b must be positive, so we can divide both sides by b:

b = (2/3)a

This implies a = (3/2)b.

Now we have the relationships: a = (3/2)b and c = (2/3)b.

To work with integer ratios, let b = 6k for some k > 0.

Then a = (3/2)(6k) = 9k.

And c = (2/3)(6k) = 4k.

So, a:b:c = 9k:6k:4k, or simply 9:6:4.

Step 4: Check Option 3: a, 2b, 3c are in H.P.

We have a = 9k.

2b = 2(6k) = 12k.

3c = 3(4k) = 12k.

So the terms are 9k, 12k, 12k.

For x, y, z to be in Harmonic Progression (HP), their reciprocals 1/x, 1/y, 1/z must be in AP.

So, 1/(9k), 1/(12k), 1/(12k) must be in AP.

Applying the AP condition: 2 * (1/(12k)) = 1/(9k) + 1/(12k)

1/(6k) = 1/(9k) + 1/(12k)

To sum the fractions on the right, find a common denominator (36k):

1/(6k) = (4/(36k)) + (3/(36k))

1/(6k) = 7/(36k)

1/6 = 7/36

This simplifies to 6/36 = 7/36, which is false.

Therefore, a, 2b, 3c are not in H.P.

So, Option 3 is incorrect.

Step 5: Check Option 1: 18(a + b + c)² = 18(a² + b²+c²) + ab

Substitute a=9k, b=6k, c=4k into the equation.

Left Hand Side (LHS):

18(a + b + c)² = 18(9k + 6k + 4k)^2

= 18(19k)^2

= 18 * 361k^2

= 6498k^2

Right Hand Side (RHS):

18(a² + b²+c²) + ab = 18((9k)^2 + (6k)^2 + (4k)^2) + (9k)(6k)

= 18(81k^2 + 36k^2 + 16k^2) + 54k^2

= 18(133k^2) + 54k^2

= 2394k^2 + 54k^2

= 2448k^2

Since LHS (6498k^2) is not equal to RHS (2448k^2), the statement is false.

So, Option 1 is incorrect.

Step 6: Check Option 4: a, b, c can be the lengths of the sides of a triangle

For a, b, c to be the lengths of the sides of a triangle, they must satisfy the triangle inequality theorem: the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Using a = 9k, b = 6k, c = 4k (where k > 0):

1. a + b > c: 9k + 6k = 15k. Is 15k > 4k? Yes.
2. a + c > b: 9k + 4k = 13k. Is 13k > 6k? Yes.
3. b + c > a: 6k + 4k = 10k. Is 10k > 9k? Yes.

All three triangle inequalities are satisfied.

Therefore, a, b, c can be the lengths of the sides of a triangle.

So, Option 4 is correct.

Conclusion:

Options 2 and 4 are correct.

The final answer is $\boxed{\text{a, b, c are in G.P., a, b, c can be the lengths of the sides of a triangle}}$

Explanation of the solution:

1. From log a, log b, log c being in AP, we deduce 2 log b = log a + log c, which simplifies to b^2 = ac. This means a, b, c are in G.P.

2. From (log a - log 2b), (log 2b - log 3c), (log 3c - log a) being in AP, we apply the AP property 2 * (middle term) = (sum of outer terms). This leads to log 2b = log 3c, implying 2b = 3c.

3. Combining b^2 = ac and 2b = 3c, we find the relationships a = (3/2)b and c = (2/3)b. This establishes the ratio a:b:c = 9:6:4.

4. Using this ratio (e.g., a=9k, b=6k, c=4k), we test the given options.

   • Option 2 (a, b, c are in G.P.) is confirmed by b^2=ac.
   • Option 3 (a, 2b, 3c are in H.P.) is checked by verifying if their reciprocals are in AP. The terms 9k, 12k, 12k do not form an HP.
   • Option 1 (18(a + b + c)² = 18(a² + b²+c²) + ab) is checked by direct substitution and found to be false.
   • Option 4 (a, b, c can be the lengths of the sides of a triangle) is checked using the triangle inequality theorem (a+b>c, a+c>b, b+c>a). All conditions are satisfied, so this option is true.

Answer:

The correct options are:

• a, b, c are in G.P.
• a, b, c can be the lengths of the sides of a triangle