Question
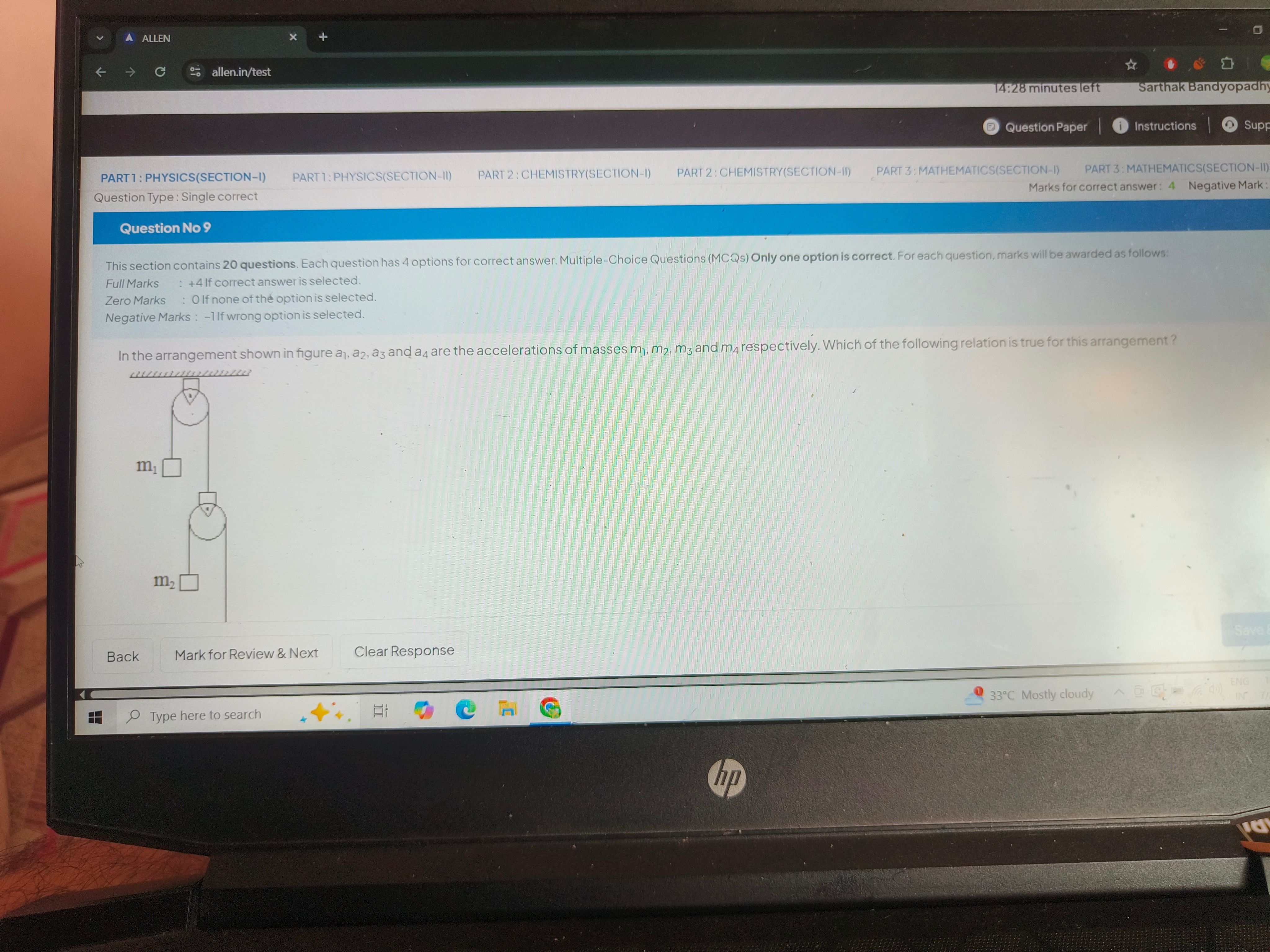
Question: In the arrangement shown in figure $a_1, a_2, a_3$ and $a_4$ are the accelerations of masses $m_1, m...
In the arrangement shown in figure a1,a2,a3 and a4 are the accelerations of masses m1,m2,m3 and m4 respectively. Which of the following relation is true for this arrangement?
a_1 + 2a_2 = 0
Solution
To determine the relation between the accelerations of the masses, we use the constraint due to the inextensibility of the string.
Let's define a coordinate system. Let the fixed ceiling be the origin (y=0). We will define downward as the positive direction for positions and accelerations.
-
Positions of the masses and pulleys:
- Let y1 be the position of mass m1 from the ceiling.
- Let yP be the position of the movable pulley from the ceiling.
- Mass m2 is attached directly to the movable pulley, so its position y2 is the same as the position of the movable pulley, i.e., y2=yP.
-
Length of the string: The string passes over the fixed pulley and then around the movable pulley. One end of the string is attached to mass m1, and the other end is attached to the ceiling.
- The segment of the string connecting mass m1 to the fixed pulley has a length proportional to y1. Let's assume the fixed pulley is at y=0. Then this length is y1.
- The segment of the string connecting the fixed pulley to the movable pulley has a length proportional to yP. This length is yP.
- The segment of the string connecting the movable pulley to the ceiling attachment point also has a length proportional to yP. This length is also yP.
- There are also constant lengths of the string that are in contact with the fixed and movable pulleys. Let this constant length be C.
The total length of the string, L, is constant: L=y1+yP+yP+C L=y1+2yP+C
-
Differentiating to find velocities and accelerations: Since the string is inextensible, its total length L is constant. Differentiating the equation for L with respect to time (t): dtdL=dtdy1+2dtdyP+dtdC Since L and C are constants, dtdL=0 and dtdC=0. So, 0=v1+2vP, where v1=dtdy1 is the velocity of m1, and vP=dtdyP is the velocity of the movable pulley.
Differentiating again with respect to time to find accelerations: dtd(0)=dtdv1+2dtdvP 0=a1+2aP, where a1=dtdv1 is the acceleration of m1, and aP=dtdvP is the acceleration of the movable pulley.
-
Relating pulley acceleration to mass acceleration: Since mass m2 is attached directly to the movable pulley, its acceleration a2 is the same as the acceleration of the movable pulley: a2=aP
-
Final relation: Substitute aP=a2 into the equation from step 3: a1+2a2=0
This relation indicates that if m1 accelerates downwards (positive a1), then m2 accelerates upwards (negative a2), and the magnitude of a1 is twice the magnitude of a2.
The question mentions a3 and a4 for masses m3 and m4, but the diagram only shows m1 and m2. It is highly probable that the mention of m3 and m4 is a typo or refers to an unpictured part of a larger system, and the intended question is to find the relation between a1 and a2 for the given setup.
The final answer is a1+2a2=0.
Explanation of the Solution:
The system consists of an inextensible string passing over a fixed pulley and a movable pulley. By defining positions from a fixed reference (e.g., the ceiling) and using the constant length of the string, a kinematic constraint equation is derived. Let y1 be the position of m1 and yP be the position of the movable pulley (which is the same as y2 for m2). The string length L=y1+2yP+constant. Differentiating this equation twice with respect to time yields 0=a1+2aP. Since aP=a2, the relation is a1+2a2=0.
