Question

In both the given cases, when blocks in contact were at rest, the forces are applied as shown. All the surfaces are smooth. Which of the following statements is correct?

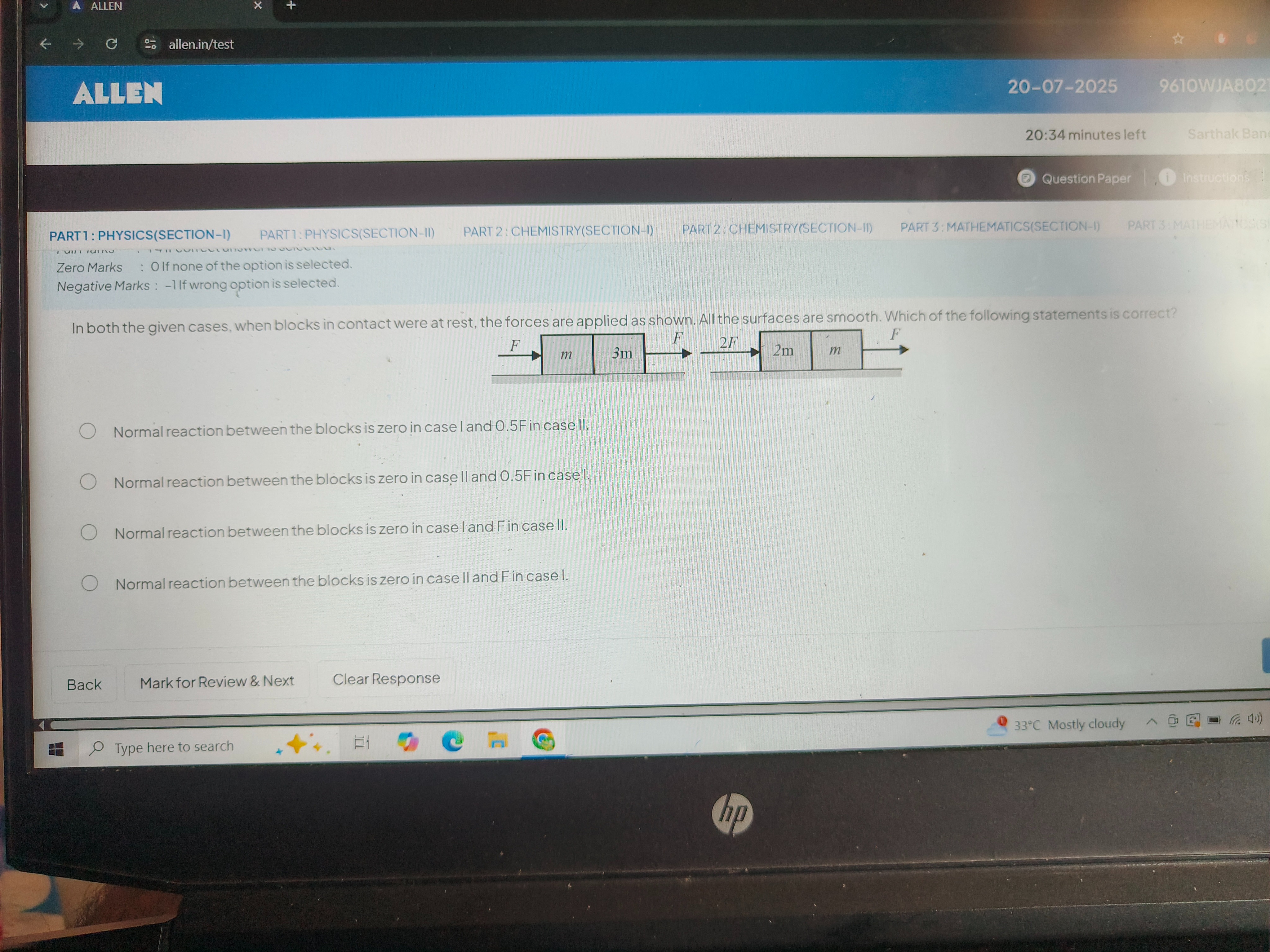
• A. Normal reaction between the blocks is zero in case I and 0.5F in case II.
• B. Normal reaction between the blocks is zero in case II and 0.5F in case I.
• C. Normal reaction between the blocks is zero in case l'and F in case II.
• D. Normal reaction between the blocks is zero in case II and F in case I.

Answer 1

None of the options are correct. The normal reaction in Case I is 3F/4, and in Case II it is 4F/3.

Answer 2

Case I: Blocks m and 3m with force F on m

1. System Acceleration: Treat m and 3m as a single system with total mass M_I = m + 3m = 4m. The net external force is F. Using Newton's second law, the acceleration a_I of the system is:

   $F = M_I \cdot a_I$

   $F = 4m \cdot a_I$

   $a_I = \frac{F}{4m}$

2. Normal Reaction N_I: Consider the free-body diagram of the block with mass 3m. The only horizontal force acting on it is the normal reaction N_I exerted by the block m. Applying Newton's second law to the 3m block:

   $N_I = (3m) \cdot a_I$

   Substitute $a_I$:

   $N_I = (3m) \cdot \left(\frac{F}{4m}\right)$

   $N_I = \frac{3F}{4}$

Case II: Blocks 2m and m with force 2F on 2m and F on m

1. System Acceleration: Treat 2m and m as a single system with total mass $M_{II} = 2m + m = 3m$. The net external force is $F_{net, II} = 2F - F = F$ (assuming right as positive). Using Newton's second law, the acceleration $a_{II}$ of the system is:

   $F = M_{II} \cdot a_{II}$

   $F = 3m \cdot a_{II}$

   $a_{II} = \frac{F}{3m}$

2. Normal Reaction N_{II}: Consider the free-body diagram of the block with mass m. The forces acting on it are the normal reaction $N_{II}$ exerted by the block 2m (to the right) and the applied force F (to the left). Applying Newton's second law to the m block:

   $N_{II} - F = m \cdot a_{II}$

   Substitute $a_{II}$:

   $N_{II} - F = m \cdot \left(\frac{F}{3m}\right)$

   $N_{II} - F = \frac{F}{3}$

   $N_{II} = F + \frac{F}{3}$

   $N_{II} = \frac{4F}{3}$

Summary of Results:

Normal reaction in Case I ($N_I$) = $\frac{3F}{4}$

Normal reaction in Case II ($N_{II}$) = $\frac{4F}{3}$

Upon comparing these results with the given options, none of the options match the calculated values. Furthermore, options stating "Normal reaction between the blocks is zero" are physically incorrect for the given scenarios, as the forces are pushing the blocks together on smooth surfaces, which would result in contact forces and acceleration.

The question appears to be flawed as none of the provided options are correct based on standard physics principles.