Question

A monkey of mass 2 kg is climbing up a rope with an acceleration of 3 ms-2. Find the tension in the rope in the portion AB and BC. (take g = 10 ms-2)

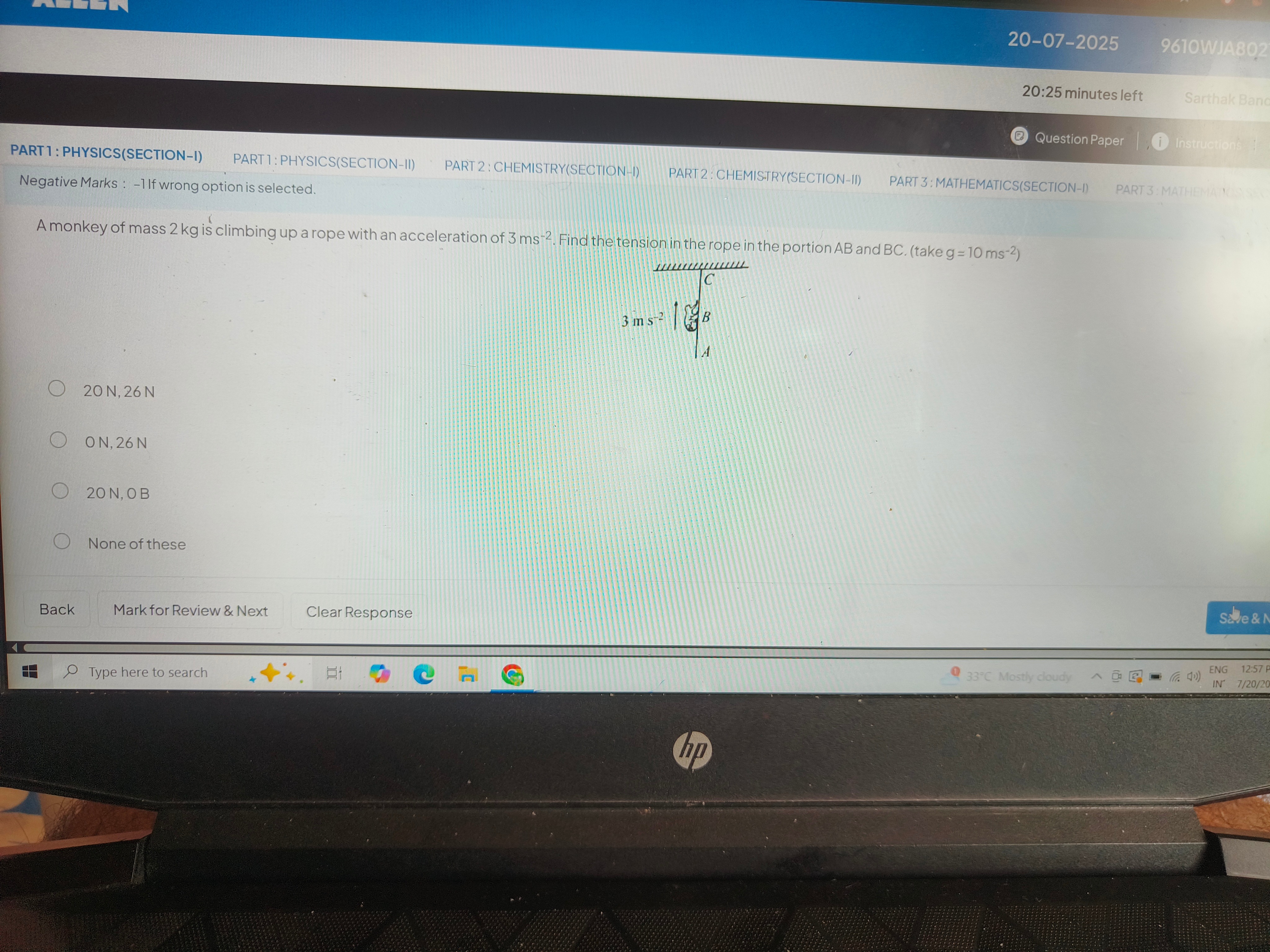
• A. 20 N, 26 N
• B. 0 N, 26 N
• C. 20 N, 0 B
• D. None of these

Answer 1

Answer: (B)

0 N, 26 N

Answer 2

To solve this problem, we need to apply Newton's second law of motion. The problem states that a monkey of mass 2 kg is climbing up a rope with an acceleration of 3 m/s². We are given g = 10 m/s². We need to find the tension in two portions of the rope, AB and BC.

First, let's determine the force the monkey exerts on the rope (which is equal to the tension in the rope segment directly supporting the monkey).

1. Free Body Diagram of the Monkey: Let T be the upward tension force exerted by the rope on the monkey. The downward force on the monkey is its weight, $mg$. The monkey is accelerating upwards with acceleration $a$.

Applying Newton's second law ($\Sigma F = ma$): $T - mg = ma$ $T = mg + ma$ $T = m(g + a)$

Substitute the given values: Mass of monkey ($m$) = 2 kg Acceleration due to gravity ($g$) = 10 m/s² Acceleration of monkey ($a$) = 3 m/s²

$T = 2 \text{ kg} \times (10 \text{ m/s}^2 + 3 \text{ m/s}^2)$ $T = 2 \text{ kg} \times (13 \text{ m/s}^2)$ $T = 26 \text{ N}$

This tension (26 N) is the force transmitted through the rope due to the monkey's action.

2. Interpretation of Portions AB and BC: The diagram shows the rope fixed at point C, with a segment BC and a segment AB below it, and the monkey at point A, which is the lowest end. If the monkey is at point A, then the entire rope above A (segments AB and BC) would be under the same tension, which is 26 N (assuming the rope is massless). In this case, $T_{AB} = 26 \text{ N}$ and $T_{BC} = 26 \text{ N}$. However, (26 N, 26 N) is not among the given options.

Let's consider an alternative interpretation, which is common in such problems when distinct tensions are asked for different segments. This implies that the monkey is located between points A and C. Given the options, the most plausible scenario is that the monkey is at point B.

Scenario: Monkey is at point B

• Tension in portion BC ($T_{BC}$): The segment BC is above the monkey. This portion of the rope must support the monkey's weight and provide the necessary force for its upward acceleration. Therefore, the tension in portion BC is the force we calculated earlier: $T_{BC} = T = 26 \text{ N}$

• Tension in portion AB ($T_{AB}$): The segment AB is below the monkey (at B). Since the rope is assumed to be massless and there is nothing attached to the rope at point A (the free end below the monkey), there is no force pulling on the segment AB from below. Thus, the tension in portion AB is zero. $T_{AB} = 0 \text{ N}$

Therefore, based on this interpretation, the tension in portion AB is 0 N, and the tension in portion BC is 26 N. This matches one of the given options.

The order in the question is "portion AB and BC", so the answer should be (Tension in AB, Tension in BC).

Final values: $T_{AB} = 0 \text{ N}$, $T_{BC} = 26 \text{ N}$.