Question

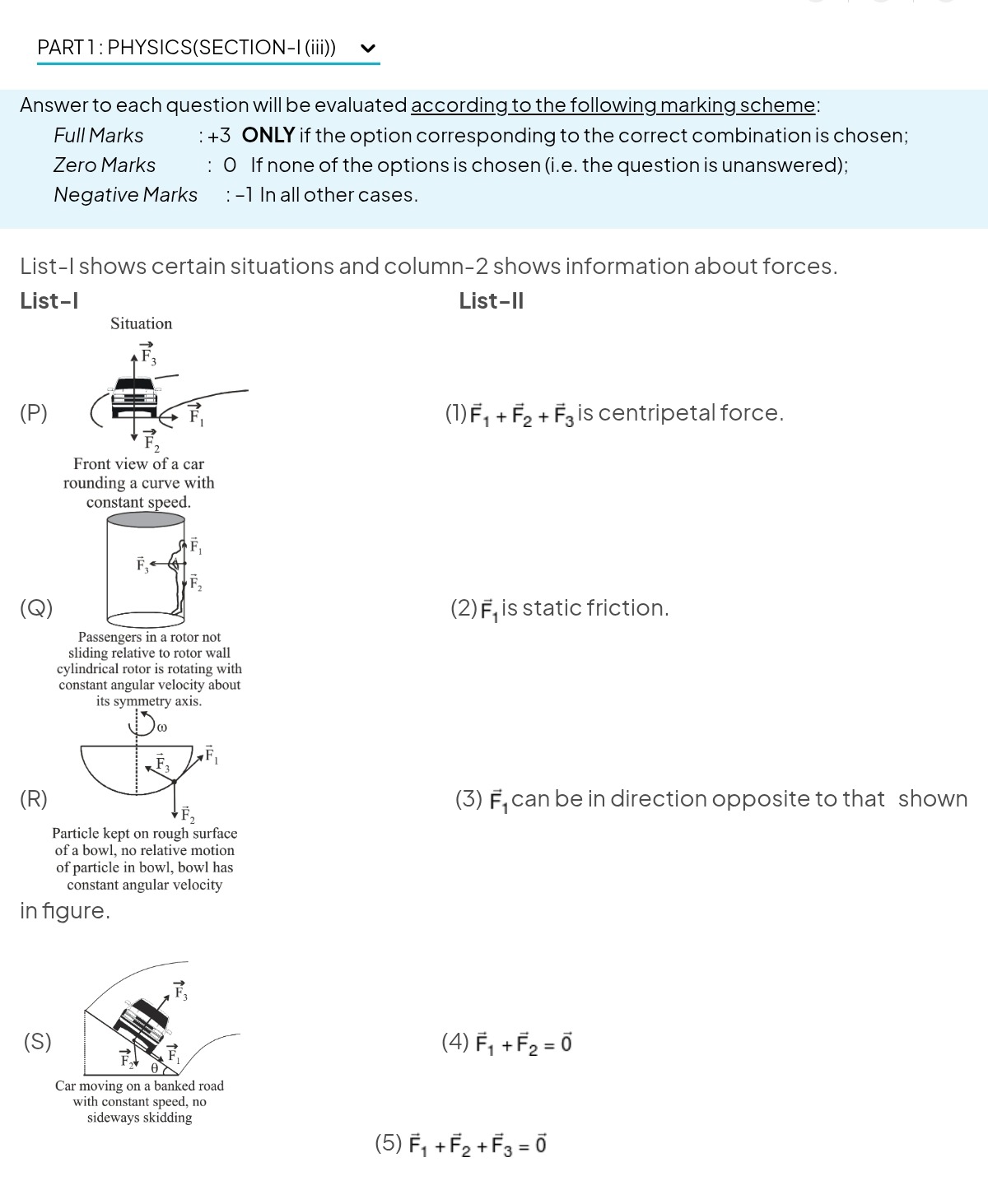
List-I shows certain situations and column-2 shows information about forces.

List-I	List-II
(P) Front view of a car rounding a curve with constant speed.	(1) $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is centripetal force.
(Q) Passengers in a rotor not sliding relative to rotor wall cylindrical rotor is rotating with constant angular velocity about its symmetry axis.	(2) $\vec{F_1}$ is static friction.
(R) Particle kept on rough surface of a bowl, no relative motion of particle in bowl, bowl has constant angular velocity in figure.	(3) $\vec{F_1}$ can be in direction opposite to that shown
(S) Car moving on a banked road with constant speed, no sideways skidding	(4) $\vec{F_1}+\vec{F_2}=\vec{0}$
(5) $\vec{F_1}+\vec{F_2}+\vec{F_3}=\vec{0}$

• A. (P)-(1), (2); (Q)-(1), (2); (R)-(1), (2), (3); (S)-(1), (2), (3)
• B. (P)-(1), (2); (Q)-(1), (2); (R)-(1), (2); (S)-(1), (2)
• C. (P)-(1); (Q)-(1); (R)-(1), (3); (S)-(1), (3)
• D. (P)-(1), (2), (4); (Q)-(1), (2), (5); (R)-(1), (2), (3); (S)-(1), (2), (3)

Answer 1

Answer: (A)

(P)-(1), (2); (Q)-(1), (2); (R)-(1), (2), (3); (S)-(1), (2), (3)

Answer 2

Detailed Explanation

The problem requires matching situations from List-I with information about forces from List-II. We analyze each situation:

(P) Front view of a car rounding a curve with constant speed. The car is moving in a horizontal circle. Therefore, there must be a net force towards the center of the circle, which is the centripetal force. In the diagram:

• $\vec{F_1}$ is directed towards the center of the curve. This is the force providing the centripetal acceleration.
• $\vec{F_2}$ is the normal force, acting vertically upwards.
• $\vec{F_3}$ is the gravitational force, acting vertically downwards.

For the car to move in a horizontal circle, the net force in the vertical direction must be zero (assuming the road is horizontal and the car is not moving vertically). Thus, $\vec{F_2} + \vec{F_3} = \vec{0}$. The net force acting on the car is $\vec{F_{net}} = \vec{F_1} + \vec{F_2} + \vec{F_3}$. Since $\vec{F_2} + \vec{F_3} = \vec{0}$, the net force is $\vec{F_{net}} = \vec{F_1}$. This net force $\vec{F_1}$ is the centripetal force required for circular motion.

• Match (P) with (1): $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is the net force, which equals $\vec{F_1}$ and is the centripetal force. So, $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is centripetal force.
• Match (P) with (2): The force $\vec{F_1}$ towards the center is provided by the static friction between the tires and the road. So, $\vec{F_1}$ is static friction.
• Option (3) is incorrect because $\vec{F_1}$ must be towards the center for turning.
• Option (4) is incorrect because $\vec{F_1}$ and $\vec{F_2}$ are perpendicular.
• Option (5) is incorrect because the net force is not zero; it is the centripetal force.

(Q) Passengers in a rotor not sliding relative to rotor wall. The person is moving in a horizontal circle due to the rotation of the cylindrical rotor. In the diagram:

• $\vec{F_1}$ is directed upwards, parallel to the rotor wall. This is the static friction.
• $\vec{F_2}$ is directed radially inwards, perpendicular to the rotor wall. This is the normal force, which provides the centripetal force.
• $\vec{F_3}$ is directed downwards, representing the gravitational force.

For the person not to slide, the upward static friction $\vec{F_1}$ must balance the downward gravitational force $\vec{F_3}$. So, $\vec{F_1} + \vec{F_3} = \vec{0}$ (in the vertical direction). The net force on the person is $\vec{F_{net}} = \vec{F_1} + \vec{F_2} + \vec{F_3}$. Since $\vec{F_1} + \vec{F_3} = \vec{0}$, the net force is $\vec{F_{net}} = \vec{F_2}$. This net force $\vec{F_2}$ is the centripetal force required for circular motion.

• Match (Q) with (1): $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is the net force, which equals $\vec{F_2}$ and is the centripetal force. So, $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is centripetal force.
• Match (Q) with (2): $\vec{F_1}$ is the upward force preventing the person from sliding down, which is static friction.
• Option (3) is incorrect because gravity is downwards, so friction must be upwards to prevent sliding.
• Option (4) is incorrect because $\vec{F_1}$ is vertical and $\vec{F_2}$ is horizontal.
• Option (5) is incorrect because the net force is the centripetal force $\vec{F_2}$, not zero.

(R) Particle kept on rough surface of a bowl, no relative motion of particle in bowl, bowl has constant angular velocity. The particle moves in a horizontal circle. In the diagram:

• $\vec{F_1}$ is directed upwards along the surface of the bowl. This is the static friction.
• $\vec{F_2}$ is the normal force, perpendicular to the surface of the bowl.
• $\vec{F_3}$ is the gravitational force, acting downwards.

The net force on the particle is $\vec{F_{net}} = \vec{F_1} + \vec{F_2} + \vec{F_3}$. This net force provides the centripetal acceleration.

• Match (R) with (1): The sum of all forces $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is the net force, which is the centripetal force.
• Match (R) with (2): $\vec{F_1}$ is shown upwards along the slope, representing static friction.
• Match (R) with (3): The direction of static friction depends on the required force. If the normal force and gravity's component are not sufficient or are excessive for the required centripetal force and vertical equilibrium, friction can act downwards along the slope. Thus, $\vec{F_1}$ can be in the direction opposite to that shown.
• Option (4) is incorrect.
• Option (5) is incorrect because the net force is not zero.

(S) Car moving on a banked road with constant speed, no sideways skidding. The car is moving in a horizontal circle on a banked road. In the diagram:

• $\vec{F_1}$ is directed upwards along the banked surface. This is the static friction.
• $\vec{F_2}$ is the normal force, perpendicular to the banked surface.
• $\vec{F_3}$ is the gravitational force, acting downwards.

The net force on the car is $\vec{F_{net}} = \vec{F_1} + \vec{F_2} + \vec{F_3}$. This net force provides the centripetal acceleration.

• Match (S) with (1): The sum of all forces $\vec{F_1}+\vec{F_2}+\vec{F_3}$ is the net force, which is the centripetal force.
• Match (S) with (2): $\vec{F_1}$ is shown upwards along the slope, representing static friction.
• Match (S) with (3): If the car's speed is higher than the ideal speed for the banking, the car tends to slide outwards, and friction acts downwards along the slope. Thus, $\vec{F_1}$ can be in the direction opposite to that shown.
• Option (4) is incorrect.
• Option (5) is incorrect because the net force is not zero.

The correct matches are:

• (P) $\leftrightarrow$ (1), (2)
• (Q) $\leftrightarrow$ (1), (2)
• (R) $\leftrightarrow$ (1), (2), (3)
• (S) $\leftrightarrow$ (1), (2), (3)