Question
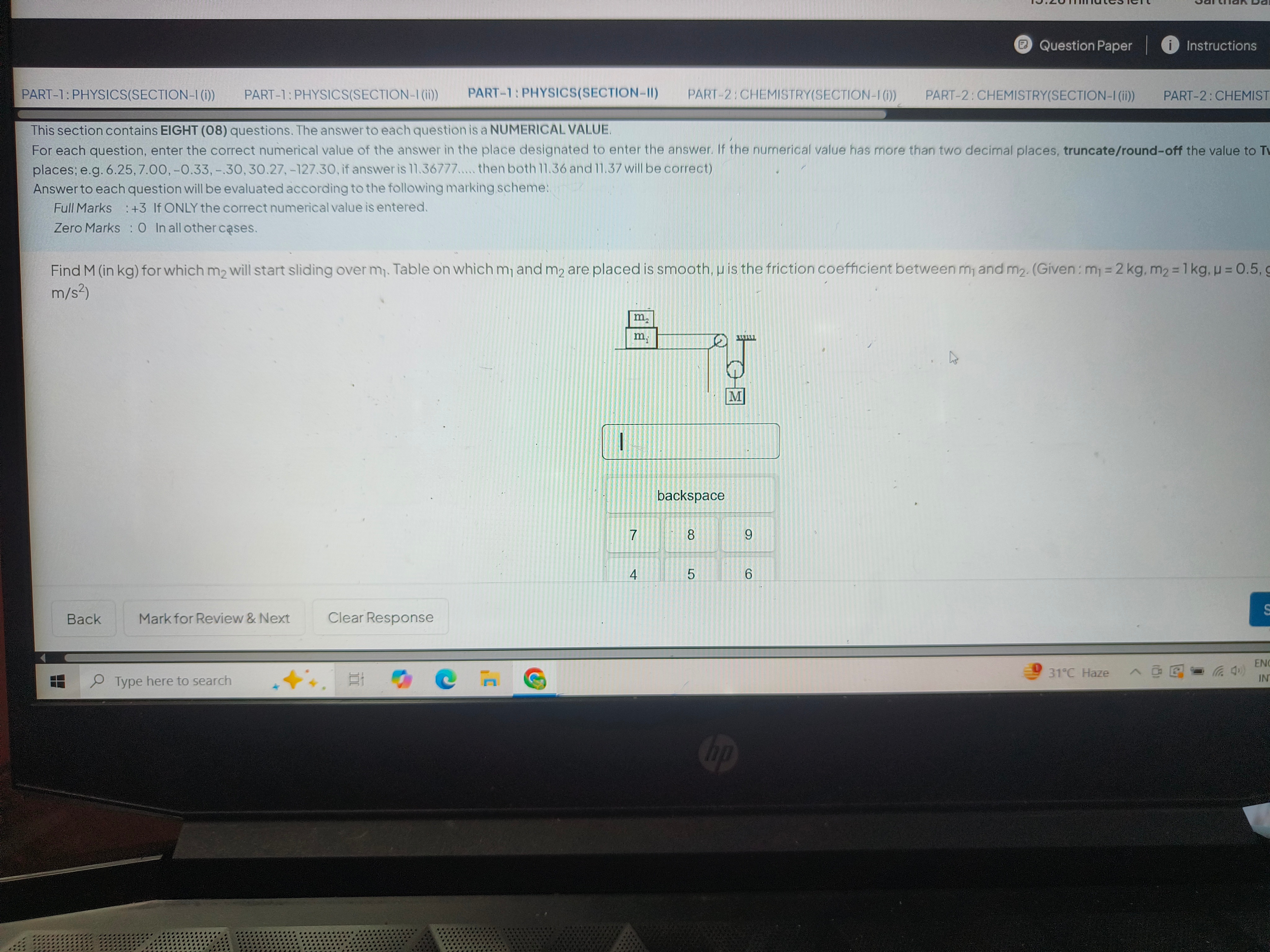
Question: Find M (in kg) for which m₂ will start sliding over m₁. Table on which m₁ and m₂ are placed is smoot...
Find M (in kg) for which m₂ will start sliding over m₁. Table on which m₁ and m₂ are placed is smooth, μ is the friction coefficient between m₁ and m2. (Given : m₁ = 2 kg, m2 = 1 kg, μ = 0.5, g = 10 m/s²)
3.00
Solution
To find the mass M for which m₂ will start sliding over m₁, we need to consider the forces acting on the system and the condition for relative motion.
1. Condition for m₂ to start sliding: For m₂ to move without sliding over m₁, the static friction force between m₁ and m₂ must provide the necessary acceleration to m₂. The maximum static friction force (fs,max) between m₁ and m₂ is given by: fs,max=μN2 Where N2 is the normal force exerted by m₁ on m₂. Since m₂ is on a horizontal surface (m₁), N2=m2g. So, fs,max=μm2g
The maximum acceleration (amax) that m₂ can have without sliding over m₁ is when the static friction force reaches its maximum value. From Newton's second law for m₂: fs,max=m2amax μm2g=m2amax amax=μg
So, m₂ will start sliding over m₁ when the acceleration of the system (m₁ and m₂ moving together) exceeds amax=μg. Therefore, the critical condition for m₂ to just start sliding is when the acceleration of the system is exactly a=μg.
2. Acceleration of the system (m₁ + m₂ + M): Consider the entire system consisting of masses m₁, m₂, and M. The table on which m₁ and m₂ are placed is smooth, so there is no friction from the table. The only external horizontal force acting on the (m₁ + m₂) block is the tension from the string, which is ultimately due to the weight of mass M. The total mass being accelerated is (m1+m2+M). The net force causing the acceleration is the weight of mass M, which is Mg. Using Newton's second law for the entire system: Fnet=(m1+m2+M)a Mg=(m1+m2+M)a So, the acceleration of the system is: a=m1+m2+MMg
3. Equating the accelerations to find M: For m₂ to just start sliding over m₁, the acceleration of the system must be equal to amax: a=amax m1+m2+MMg=μg
Cancel 'g' from both sides (assuming g=0): m1+m2+MM=μ
Now, substitute the given values: m₁ = 2 kg m₂ = 1 kg μ = 0.5
2+1+MM=0.5 3+MM=0.5
Cross-multiply: M=0.5(3+M) M=1.5+0.5M M−0.5M=1.5 0.5M=1.5 M=0.51.5 M=3 kg
Thus, m₂ will start sliding over m₁ when M is 3 kg.
