Question

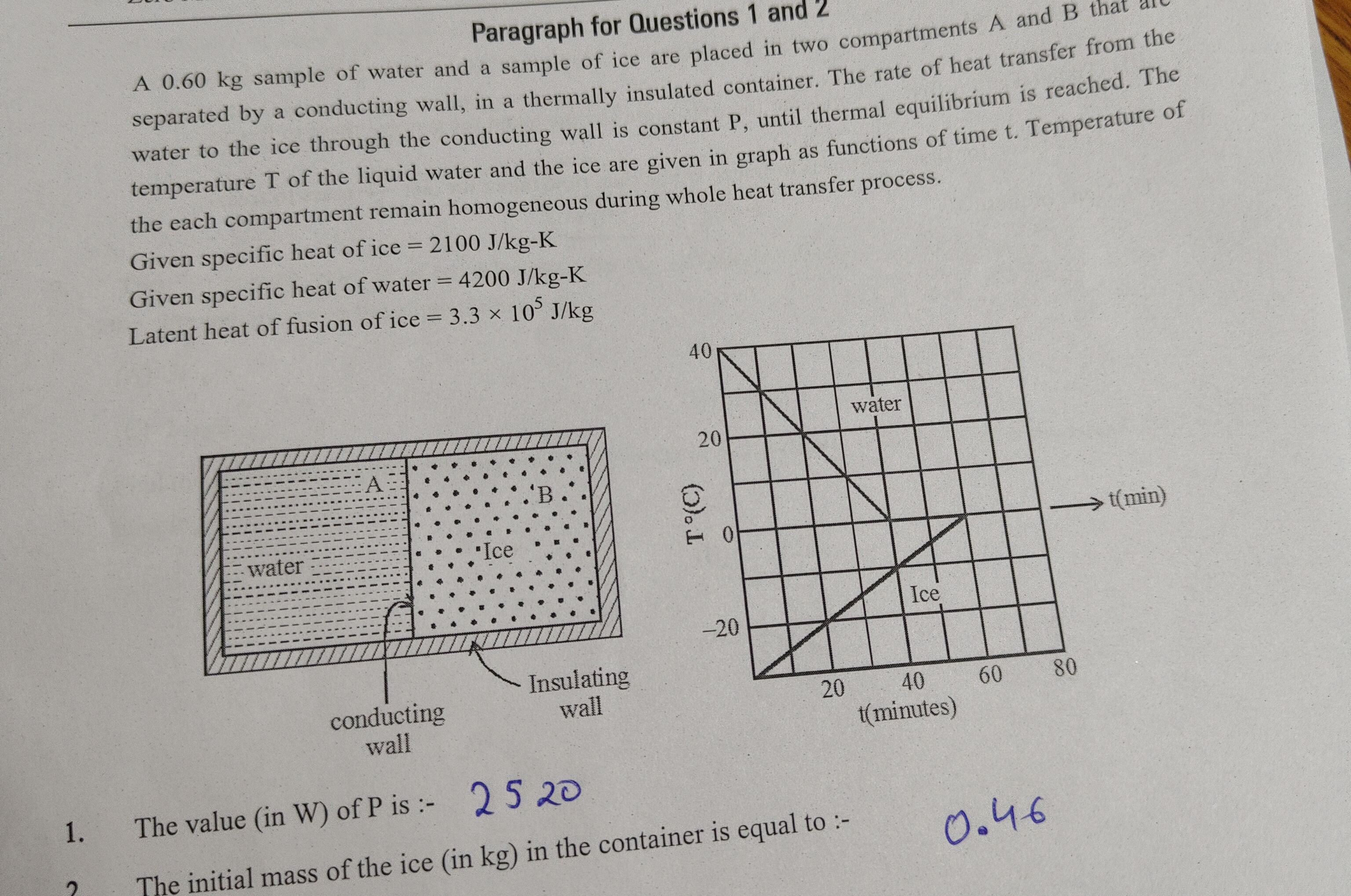
Paragraph for Questions 1 and 2 A 0.60 kg sample of water and a sample of ice are placed in two compartments A and B that are separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the each compartment remain homogeneous during whole heat transfer process.

Given specific heat of ice = 2100 J/kg-K Given specific heat of water = 4200 J/kg-K Latent heat of fusion of ice = 3.3 × 10⁵ J/kg

1. The value (in W) of P is :-
2. The initial mass of the ice (in kg) in the container is equal to :-

• A. 25
• B. 20
• C. 42
• D. 0.46

Answer 1

Answer: (C)

42

Answer 2

The rate of heat transfer $P$ can be calculated from the heat lost by the water as it cools from $40^\circ\text{C}$ to $0^\circ\text{C}$ in $40$ minutes. Mass of water, $m_w = 0.60$ kg. Specific heat of water, $c_w = 4200$ J/kg-K. Temperature change of water, $\Delta T_w = 40^\circ\text{C} - 0^\circ\text{C} = 40$ K. Time taken, $\Delta t = 40$ minutes $= 40 \times 60$ seconds $= 2400$ seconds.

The heat lost by the water is: $\Delta Q_w = m_w \times c_w \times \Delta T_w$ $\Delta Q_w = 0.60 \text{ kg} \times 4200 \text{ J/kg-K} \times 40 \text{ K} = 100800 \text{ J}$

The rate of heat transfer $P$ is: $P = \frac{\Delta Q_w}{\Delta t} = \frac{100800 \text{ J}}{2400 \text{ s}} = 42 \text{ W}$

For the second part of the question, we use the calculated rate of heat transfer $P = 42$ W. The ice warms from $-20^\circ\text{C}$ to $0^\circ\text{C}$ in $40$ minutes. Specific heat of ice, $c_i = 2100$ J/kg-K. Temperature change of ice, $\Delta T_i = 0^\circ\text{C} - (-20^\circ\text{C}) = 20$ K. Time taken, $\Delta t = 2400$ seconds.

The heat gained by the ice is: $\Delta Q_i = m_i \times c_i \times \Delta T_i$ Where $m_i$ is the initial mass of ice.

The rate of heat transfer $P$ is also equal to the heat gained by the ice divided by the time: $P = \frac{\Delta Q_i}{\Delta t}$ $42 \text{ W} = \frac{m_i \times 2100 \text{ J/kg-K} \times 20 \text{ K}}{2400 \text{ s}}$ $42 = \frac{m_i \times 42000}{2400}$ $m_i = \frac{42 \times 2400}{42000} = \frac{2.4 \times 42}{42} = 2.4 \text{ kg}$

Note: There is a discrepancy with the handwritten answers provided in the original problem. The solution above is derived from a consistent application of physics principles to the given graph and parameters. The question asks for the value of P, which is 42 W.