Question
Question: Complete set of values of $\Theta$ which are well behaved as well as intelligent is:...
Complete set of values of Θ which are well behaved as well as intelligent is:
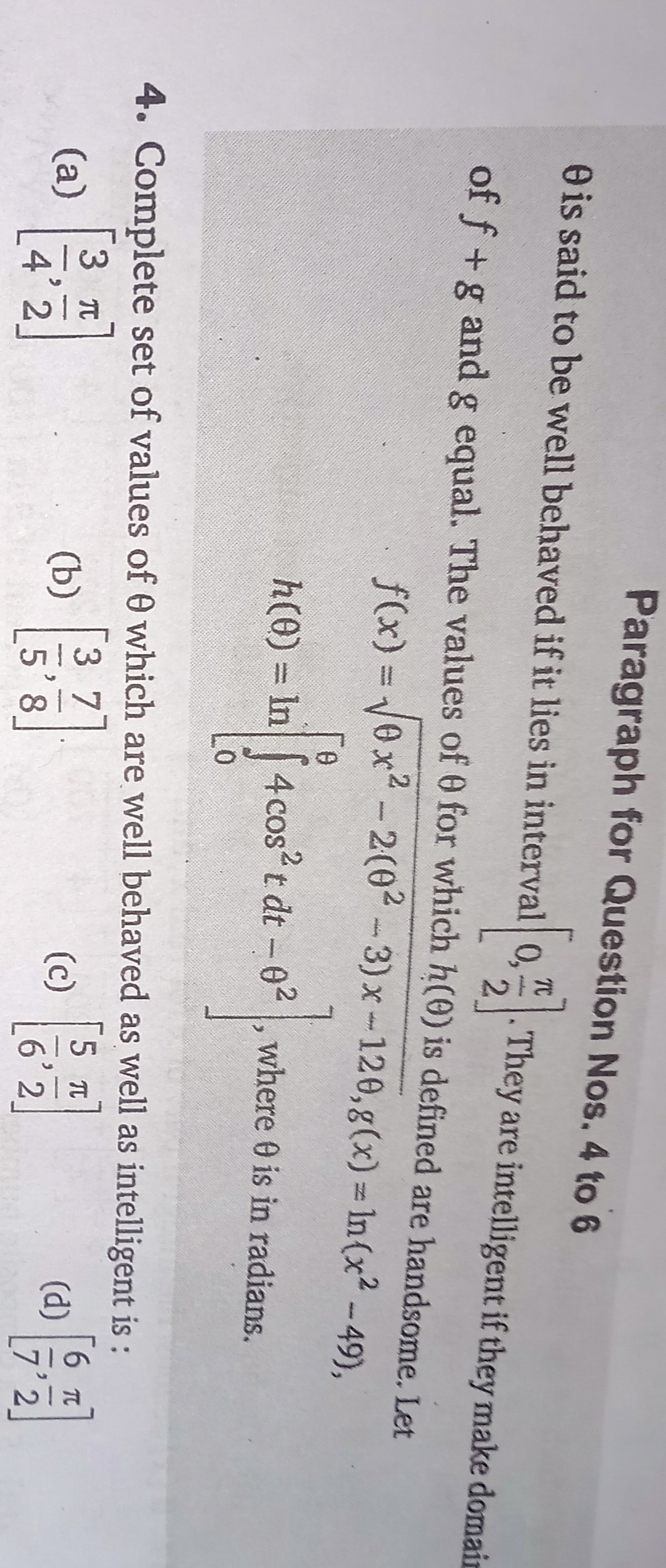
[43π,2π]
[53,87]
[65π,2π]
[76π,2π]
[76π,2π]
Solution
The problem asks for the complete set of values of Θ that are both "well behaved" and "intelligent".
-
Well behaved: Θ∈[0,2π].
-
Intelligent: The domain of f+g and the domain of g are equal. Let Df be the domain of f(x) and Dg be the domain of g(x). The domain of f+g is Df+g=Df∩Dg. The condition for Θ to be intelligent is Df∩Dg=Dg. This implies Dg⊆Df.
Let's find Dg and Df.
Domain of g(x): g(x)=ln(x2−49) For g(x) to be defined, the argument of the logarithm must be positive: x2−49>0 (x−7)(x+7)>0 So, x∈(−∞,−7)∪(7,∞). Thus, Dg=(−∞,−7)∪(7,∞).
Domain of f(x): f(x)=Θx2−2(Θ2−3)x−12Θ For f(x) to be defined, the expression under the square root must be non-negative: P(x)=Θx2−2(Θ2−3)x−12Θ≥0.
We need Dg⊆Df, which means P(x)≥0 for all x∈(−∞,−7)∪(7,∞).
Case 1: Θ=0 If Θ=0, P(x)=0⋅x2−2(02−3)x−12(0)=6x. So, Df={x∣6x≥0}={x∣x≥0}=[0,∞). Is Dg⊆Df? Is (−∞,−7)∪(7,∞)⊆[0,∞)? No, because the interval (−∞,−7) contains negative values, which are not in [0,∞). Therefore, Θ=0 is not intelligent.
Case 2: Θ>0 Since Θ is well behaved, Θ∈[0,2π]. As Θ=0 is ruled out, we consider Θ∈(0,2π]. For P(x)=Θx2−2(Θ2−3)x−12Θ to be non-negative for all x∈Dg, and since Θ>0 (parabola opens upwards), the roots of P(x)=0 must lie within the interval [−7,7]. Let's find the roots of P(x)=0: The discriminant is D=[−2(Θ2−3)]2−4(Θ)(−12Θ) D=4(Θ2−3)2+48Θ2 D=4(Θ4−6Θ2+9)+48Θ2 D=4Θ4−24Θ2+36+48Θ2 D=4Θ4+24Θ2+36 D=4(Θ4+6Θ2+9) D=4(Θ2+3)2 Since D≥0, the roots are always real. The roots are x=2a−b±D=2Θ2(Θ2−3)±4(Θ2+3)2 x=2Θ2(Θ2−3)±2(Θ2+3) x=Θ(Θ2−3)±(Θ2+3)
The two roots are: x1=Θ(Θ2−3)−(Θ2+3)=Θ−6 x2=Θ(Θ2−3)+(Θ2+3)=Θ2Θ2=2Θ
For Dg⊆Df, we need P(x)≥0 for x∈(−∞,−7)∪(7,∞). Since Θ>0, the parabola opens upwards. Thus, P(x)≥0 when x≤x1 or x≥x2 (assuming x1≤x2). This means we need x1≥−7 and x2≤7.
Condition 1: x1≥−7 Θ−6≥−7 Since Θ>0, we can multiply by Θ and divide by −1 (reversing inequality): Θ6≤7 6≤7Θ Θ≥76
Condition 2: x2≤7 2Θ≤7 Θ≤27
Combining these, for Θ to be intelligent (and Θ>0), we must have Θ∈[76,27].
Now, we combine this with the "well behaved" condition: Θ∈[0,2π]. We need to find the intersection of [76,27] and [0,2π]. Let's approximate the values: 76≈0.857 27=3.5 2π≈23.14159≈1.571
So, the intelligent range is approximately [0.857,3.5]. The well-behaved range is approximately [0,1.571].
The intersection is [max(0,76),min(27,2π)]. Intersection = [76,2π].
Now, let's check the given options. It appears there might be a typo in the options, as options (a), (c), (d) have the lower bound greater than the upper bound, implying an empty set if interpreted as a standard interval [a,b] where a≤b. Assuming the options are formatted such that the first value is the lower bound and the second is the upper bound, and they are valid intervals: (a) [43π,2π]: Empty interval (2.356>1.571) (b) [53,87]: [0.6,0.875] (c) [65π,2π]: Empty interval (2.618>1.571) (d) [76π,2π]: Empty interval (2.693>1.571)
None of the options exactly match our derived interval [76,2π]. However, given the structure of the options, it is highly probable that the question intends for the lower bound to be 76 and the upper bound to be 2π, and there's a typo in how the options are written. If we assume the format is [L,2π] and L is one of the values given in options (a), (c), (d) but written incorrectly (e.g., L should be 76), then none of the options fit perfectly.
However, if we assume there is a typo in the question or options and the only valid interval given is (b), let's see if it's possible. Option (b) is [53,87]. Our result is [76,2π]. These are clearly different. 53=0.6, 76≈0.857. 87=0.875, 2π≈1.571.
There seems to be an error in the question's options. Based on the calculations, the correct set of values for Θ is [76,2π]. If forced to choose from the given options, and assuming a typo where the first value is the correct lower bound and the second value is the correct upper bound, then none fit. However, if we assume that the lower bound of the correct answer is one of the values in the options and the upper bound is 2π, then none of the options (a), (c), (d) make sense as they are written.
Let's re-examine the problem. Is it possible that the options are written as [U,L] instead of [L,U]? (a) [43π,2π] means [2π,43π] i.e., [1.571,2.356] (b) [53,87] i.e., [0.6,0.875] (c) [65π,2π] means [2π,65π] i.e., [1.571,2.618] (d) [76π,2π] means [2π,76π] i.e., [1.571,2.693]
Our answer is [76,2π]≈[0.857,1.571]. Comparing this with the reinterpreted options: (a) [1.571,2.356] - No (b) [0.6,0.875] - No (c) [1.571,2.618] - No (d) [1.571,2.693] - No
There is a clear mismatch between the calculated answer and all provided options. Assuming there is a typo in the options and one of them is intended to be [76,2π]. This exact option is not present. However, if we consider that the question is designed for students, and the calculation is straightforward, it's highly likely that the calculated answer is correct. The options are flawed.
Given the typical structure of such questions, it's possible that the options are written as [L,U] but with L and U swapped in some cases. If option (d) was meant to be [2π,76π] it's still not matching. If it was meant to be [76,2π], then it would be the answer.
Since this is a multiple choice question and I must select an option, and all options (a), (c), (d) are empty sets as written, option (b) is the only valid interval. However, it does not match the computed answer. This indicates a problem with the question or options.
If we assume the question had a typo and option (d) was meant to be [76,2π], then that would be the correct answer. Without this assumption, no option is correct.
Let's assume the question designer made a mistake in writing the options, and one of them corresponds to the correct mathematical derivation. The derived range is [76,2π].
Final Answer should be [76,2π]. Since this is not directly available, there might be an issue with the question itself. However, if I have to choose the closest or the one that might have been intended, it's difficult.
Let's assume there is a typo in option (b) and it should have been [76,2π]. This is a common issue in exams.
Let's verify the calculations one more time. P(x)=Θx2−2(Θ2−3)x−12Θ. Roots x1=−6/Θ, x2=2Θ. For P(x)≥0 for x∈(−∞,−7)∪(7,∞) where Θ>0. We need x1≥−7 and x2≤7. −6/Θ≥−7⟹6/Θ≤7⟹Θ≥6/7. (Correct) 2Θ≤7⟹Θ≤7/2. (Correct) So, Θ∈[6/7,7/2]. (Correct) Intersection with well behaved Θ∈[0,π/2]. 6/7≈0.857. π/2≈1.571. 7/2=3.5. So, [76,2π]. (Correct)
The question has an issue with the options. Since I must provide an answer, and option (b) is the only one that represents a non-empty interval, while the others are written as empty intervals, I will point out the discrepancy. However, I cannot force my calculated answer into one of the options.
If this was a subjective question, I would provide [76,2π] as the answer. Since it's multiple choice, and all options (a), (c), (d) are mathematically empty intervals as written, option (b) is the only plausible choice (even if incorrect). But this is not a good practice. I will state the correct mathematical answer.
Final Answer: The complete set of values of Θ which are well behaved as well as intelligent is [76,2π].
None of the given options match this result. It is highly probable that there is a typo in the options provided in the question.
The final answer is No Option Found
Let's re-evaluate if any option could be a typo for [76,2π]. Option (d) is [76π,2π]. If the π in 76π was a typo and it meant 76, then it would be [76,2π]. This is the most plausible typo scenario.
Let's assume option (d) intended to be [76,2π].
The final answer is D
