Question

If $P(x) = \begin{vmatrix} a_1 & x & x \\ x & a_2 & x \\ x & x & a_3 \end{vmatrix} = xg(x) - f(x)$, then (where, $f(x) = (x - a_1)(x - a_2)(x - a_3)$)

Answer 1

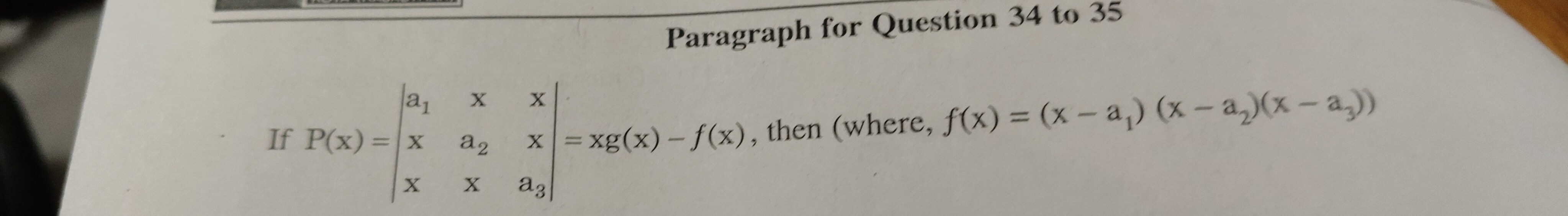
g(x) = 3x^2 - 2(a_1 + a_2 + a_3)x + (a_1 a_2 + a_1 a_3 + a_2 a_3)

Answer 2

The problem provides a determinant $P(x)$ and a relationship $P(x) = xg(x) - f(x)$, where $f(x)$ is a given polynomial. The goal is to determine the expression for $g(x)$.

1. Expand the determinant $P(x)$: $P(x) = \begin{vmatrix} a_1 & x & x \\ x & a_2 & x \\ x & x & a_3 \end{vmatrix}$

Expand along the first row: $P(x) = a_1 \begin{vmatrix} a_2 & x \\ x & a_3 \end{vmatrix} - x \begin{vmatrix} x & x \\ x & a_3 \end{vmatrix} + x \begin{vmatrix} x & a_2 \\ x & x \end{vmatrix}$ $P(x) = a_1 (a_2 a_3 - x^2) - x (x a_3 - x^2) + x (x^2 - x a_2)$ $P(x) = a_1 a_2 a_3 - a_1 x^2 - x^2 a_3 + x^3 + x^3 - x^2 a_2$ $P(x) = 2x^3 - (a_1 + a_2 + a_3)x^2 + a_1 a_2 a_3$

2. Expand the polynomial $f(x)$: $f(x) = (x - a_1)(x - a_2)(x - a_3)$ This is a standard expansion for a cubic polynomial with roots $a_1, a_2, a_3$: $f(x) = x^3 - (a_1 + a_2 + a_3)x^2 + (a_1 a_2 + a_1 a_3 + a_2 a_3)x - a_1 a_2 a_3$

3. Use the given relationship $P(x) = xg(x) - f(x)$ to find $xg(x)$: Rearrange the equation to solve for $xg(x)$: $xg(x) = P(x) + f(x)$

Substitute the expanded forms of $P(x)$ and $f(x)$: $xg(x) = [2x^3 - (a_1 + a_2 + a_3)x^2 + a_1 a_2 a_3] + [x^3 - (a_1 + a_2 + a_3)x^2 + (a_1 a_2 + a_1 a_3 + a_2 a_3)x - a_1 a_2 a_3]$

Combine like terms: $xg(x) = (2x^3 + x^3) - (a_1 + a_2 + a_3)x^2 - (a_1 + a_2 + a_3)x^2 + (a_1 a_2 + a_1 a_3 + a_2 a_3)x + (a_1 a_2 a_3 - a_1 a_2 a_3)$ $xg(x) = 3x^3 - 2(a_1 + a_2 + a_3)x^2 + (a_1 a_2 + a_1 a_3 + a_2 a_3)x$

4. Determine $g(x)$ by dividing by $x$: Factor out $x$ from the expression for $xg(x)$: $xg(x) = x [3x^2 - 2(a_1 + a_2 + a_3)x + (a_1 a_2 + a_1 a_3 + a_2 a_3)]$

Therefore, $g(x)$ is: $g(x) = 3x^2 - 2(a_1 + a_2 + a_3)x + (a_1 a_2 + a_1 a_3 + a_2 a_3)$