Question

Packing Fraction in BCC lattice is:
A. $\dfrac{1}{6}\pi$
B. $\dfrac{{\sqrt 2 }}{6}\pi$
C. $\dfrac{{\sqrt 3 }}{8}\pi$
D. $\dfrac{{\sqrt 3 }}{2}$

Answer 1

Packing efficiency is defined as the ratio of the volume occupied by atoms in a unit cell by the total volume of the unit cell and the efficiency of the body-centered cubic lattice is 68% and the coordination number of this BCC lattice structure is eight. Packing efficiency is also known as the atomic packing factor.

Complete answer:
It is the fraction of volume in a crystal structure that is filled up or occupied by particles constituent. Packing efficiency has no physical dimensions hence it is a dimensionless quantity.
In a Body-centered cubic unit cell, 8 atoms are present at each corner along with one center atom in the center of the cube. Each corner atom has only one-eighth of its volume within the unit cell. So BCC has a total of 2 lattice points per unit cell.
In BCC total number of atoms per unit cell is $1 + (\dfrac{1}{8} \times 8) = 2$ ….(I)
In BCC, the center atom is touched by every corner atom. From one corner of the cube through the center and to the other corner a line is drawn and that passes through$4r$, $r$ is the radius of the atom and from the geometry length of the diagonal is $a\sqrt 3$

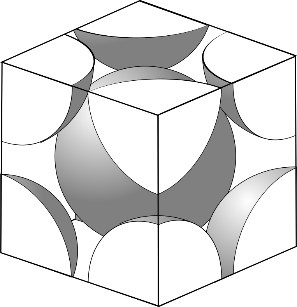
So, the length of each side of the BCC structure can be related to the radius of the atom by $a = \dfrac{{4r}}{{\sqrt 3 }}$
We know that volume of sphere $= \dfrac{4}{3}\pi {r^3}$ ….(II)
Packing efficiency =$\dfrac{{{N_{atom}}{\text{ }}{V_{atom}}}}{{{V_{unit{\text{ cell}}}}}}$ …..(III)
${N_{atom}}$is the number of atoms in a unit cell and ${V_{atom}}$ is the volume of each atom and the volume occupied by the unit cell is given by ${V_{unit{\text{ cell}}}}$
Substituting the values in equation (III)
Packing fraction$= \dfrac{{2 \times \dfrac{4}{3}\pi {r^3}}}{{{{(\dfrac{{4r}}{{\sqrt 3 }})}^3}}}$
Packing fraction in BCC lattice $= \dfrac{{\sqrt 3 }}{8}\pi$

Therefore the correct answer is option (C).

Note:
The smallest part of a component in a crystal is called a unit cell. Some of the types of crystal structures are monoclinic crystal structure, triclinic crystal structure, tetragonal crystal structure, orthorhombic crystal structure, hexagonal crystal structure and rhombohedron.