Question

One end of a necklace of small pearls is attached to the outer surface of a fixed cylinder that has radius R and a horizontal axis; the attachment point P is at the same level as the axis. The necklace is wound once round the slippery surface of the cylinder, and the free end is left to dangle (see figure). How long, $l$, does this free end need to be if the rest of the necklace is to touch the cylinder surface everywhere?

Answer 1

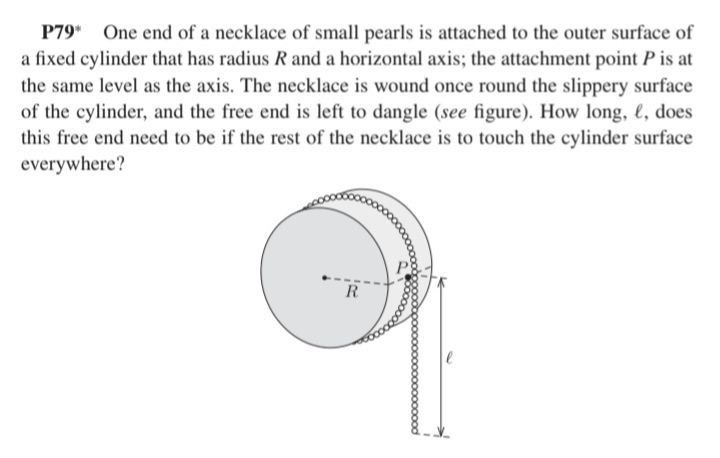
3R

Answer 2

To determine the length l of the free end such that the necklace touches the cylinder surface everywhere, we analyze the forces acting on a small element of the necklace.

Let:

• R be the radius of the cylinder.
• λ be the linear mass density of the necklace (mass per unit length).
• g be the acceleration due to gravity.

Let's define the angle θ measured clockwise from the horizontal line passing through the center of the cylinder and the attachment point P. So, P is at θ = 0. The necklace wraps once around the cylinder, meaning it covers an angular range of 2π. Since the free end dangles from the point where the necklace finishes its wrap, and the diagram shows it dangling from P, this implies the necklace starts at P, wraps around for 2π radians, and effectively ends at P. So the angular range is θ = 0 to θ = 2π.

Consider a small element of the necklace of length ds = R dθ at an angle θ. The mass of this element is dm = λ ds = λ R dθ.

The forces acting on this element are:

1. Tension T at angle θ (acting tangentially).
2. Tension T + dT at angle θ + dθ (acting tangentially).
3. Gravitational force dm g = λ R g dθ acting vertically downwards.
4. Normal force dN exerted by the cylinder, acting radially outwards.

Let's resolve forces along the tangent and normal directions. The tangential direction is along the arc, and the normal direction is radial.

1. Tangential Equilibrium: The component of gravity along the tangent (in the direction of increasing θ, which is clockwise downwards from the horizontal) is (λ R g dθ) sin θ. The change in tension dT must balance this tangential component of gravity. (T + dT) - T + λ R g dθ sin θ = 0 dT = - λ R g sin θ dθ

Integrating this equation: ∫ dT = - ∫ λ R g sin θ dθ T(θ) = λ R g cos θ + C where C is the integration constant.

2. Determining the Integration Constant C: The free end of the necklace has length l and hangs vertically. The tension at the point where the necklace leaves the cylinder (which is θ = 2π, effectively point P) is due to the weight of this dangling part. T(2π) = λ l g Substitute this into the tension equation: λ l g = λ R g cos(2π) + C Since cos(2π) = 1: λ l g = λ R g + C C = λ l g - λ R g = λ g (l - R)

So, the tension at any angle θ is: T(θ) = λ R g cos θ + λ g (l - R) T(θ) = λ g (R cos θ + l - R)

3. Normal Force Condition: For the necklace to touch the cylinder everywhere, the normal force dN must be non-negative (dN ≥ 0). Consider the forces in the radial direction (positive outwards): The radial component of tension T is T dθ (acting inwards, due to the curvature). The radial component of gravity λ R g dθ (acting vertically downwards) is (λ R g dθ) cos θ (acting inwards, towards the center). The normal force dN acts outwards.

Summing radial forces: dN - T dθ - (λ R g dθ) cos θ = 0 dN = (T + λ R g cos θ) dθ So, the normal force per unit angle is N = T + λ R g cos θ. For the necklace to touch, N ≥ 0. T(θ) + λ R g cos θ ≥ 0

Substitute T(θ): [λ g (R cos θ + l - R)] + λ R g cos θ ≥ 0 λ g R cos θ + λ g l - λ g R + λ R g cos θ ≥ 0 2λ R g cos θ + λ g (l - R) ≥ 0 2R cos θ + l - R ≥ 0 l ≥ R - 2R cos θ

For the necklace to touch the cylinder everywhere, this condition must hold for all θ in the range 0 to 2π. The term R - 2R cos θ needs to be maximized to find the minimum l. The maximum value of R - 2R cos θ occurs when cos θ is at its minimum value, which is -1. This happens at θ = π (the lowest point of the cylinder).

At θ = π: l ≥ R - 2R (-1) l ≥ R + 2R l ≥ 3R

Therefore, the minimum length l required for the necklace to touch the cylinder surface everywhere is 3R.

Explanation of the solution:

1. Define System and Coordinates: A small element of the necklace at angle θ (clockwise from horizontal at P) is considered.
2. Forces and Equilibrium: Tension T and T+dT act tangentially. Gravity λRg dθ acts vertically. Normal force dN acts radially.
3. Tangential Force Balance: dT = -λRg sinθ dθ. Integrating gives T(θ) = λRg cosθ + C.
4. Boundary Condition for Tension: The tension at the end of the necklace (at θ=2π, which is effectively P) is T(2π) = λlg. Substituting this into T(θ) gives C = λg(l-R).
5. Tension Expression: T(θ) = λg(R cosθ + l - R).
6. Normal Force Condition: For the necklace to touch the cylinder, the normal force N must be non-negative. The radial force balance gives dN = (T + λRg cosθ)dθ. So, N = T + λRg cosθ ≥ 0.
7. Minimum l: Substitute T(θ) into the normal force condition: λg(R cosθ + l - R) + λRg cosθ ≥ 0. This simplifies to 2R cosθ + l - R ≥ 0, or l ≥ R - 2R cosθ.
8. Worst Case: The minimum l must satisfy the condition for all θ. The term R - 2R cosθ is maximized when cosθ is at its minimum, i.e., cosθ = -1 (at the lowest point, θ=π).
9. Result: Substituting cosθ = -1 gives l ≥ R - 2R(-1) = 3R. Thus, the minimum length l is 3R.