Question

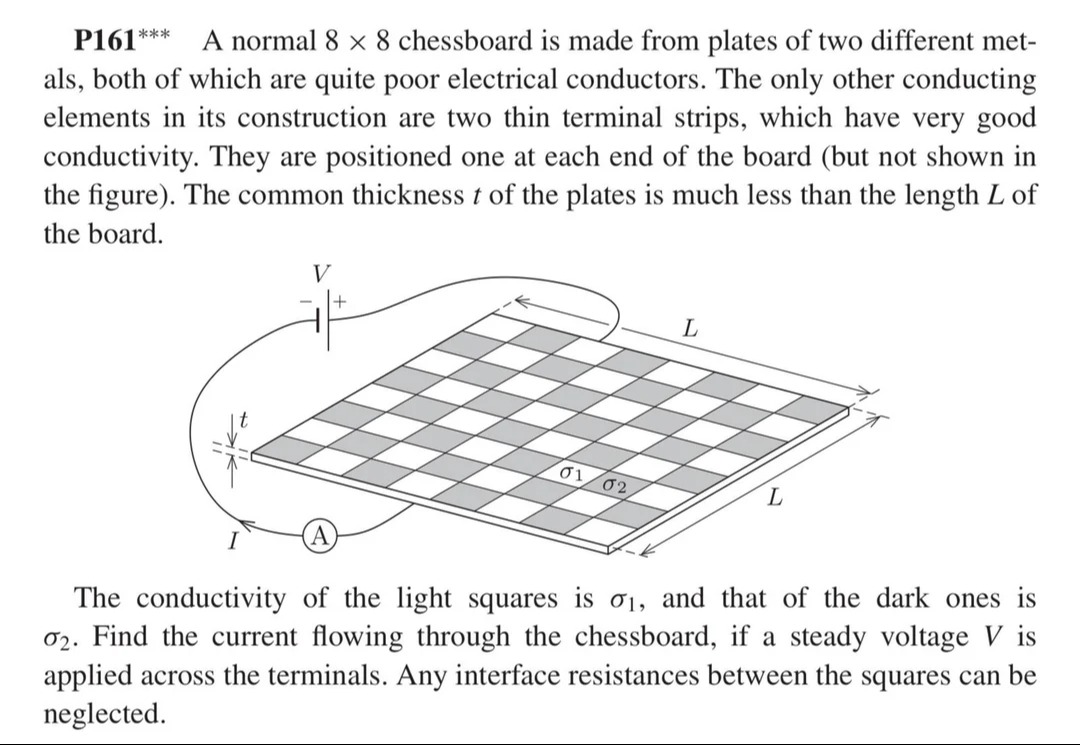
A normal 8 × 8 chessboard is made from plates of two different metals, both of which are quite poor electrical conductors. The only other conducting elements in its construction are two thin terminal strips, which have very good conductivity. They are positioned one at each end of the board (but not shown in the figure). The common thickness t of the plates is much less than the length L of the board.

The conductivity of the light squares is $\sigma_1$, and that of the dark ones is $\sigma_2$. Find the current flowing through the chessboard, if a steady voltage V is applied across the terminals. Any interface resistances between the squares can be neglected.

Answer 1

V \frac{2t \sigma_1 \sigma_2}{\sigma_1 + \sigma_2}

Answer 2

The problem describes an 8x8 chessboard made of two different metals with conductivities $\sigma_1$ and $\sigma_2$. A voltage V is applied across the ends of the board. The current flows along the length L of the board.

1. Dimensions of a single square:

   The chessboard is 8x8, and its total length is L. Therefore, the side length of each individual square is $s = L/8$. The thickness of the plates is given as $t$.

2. Resistance of a single square:

   The current flows along the length 's' of each square. The cross-sectional area perpendicular to the current flow for a single square is $A = s \times t = (L/8)t$. The resistance of a conductor is given by $R = \rho \frac{\text{length}}{\text{area}}$, where $\rho = 1/\sigma$ is the resistivity. For a light square (conductivity $\sigma_1$): $R_1 = \frac{1}{\sigma_1} \frac{s}{s \times t} = \frac{1}{\sigma_1 t}$ For a dark square (conductivity $\sigma_2$): $R_2 = \frac{1}{\sigma_2} \frac{s}{s \times t} = \frac{1}{\sigma_2 t}$

3. Resistance of a single row:

   A chessboard has alternating light and dark squares. In an 8x8 board, each row consists of 8 squares. Since they alternate, there will be 4 squares of type $\sigma_1$ and 4 squares of type $\sigma_2$ in each row. These squares are connected in series along the direction of current flow. The total resistance of one row ($R_{row}$) is the sum of the resistances of these 8 squares: $R_{row} = 4R_1 + 4R_2$ $R_{row} = 4 \left( \frac{1}{\sigma_1 t} \right) + 4 \left( \frac{1}{\sigma_2 t} \right)$ $R_{row} = \frac{4}{t} \left( \frac{1}{\sigma_1} + \frac{1}{\sigma_2} \right)$ $R_{row} = \frac{4}{t} \left( \frac{\sigma_1 + \sigma_2}{\sigma_1 \sigma_2} \right)$

4. Equivalent resistance of the chessboard:

   The 8 rows of the chessboard are connected in parallel across the voltage V. Since all rows are identical, the equivalent resistance ($R_{eq}$) of the entire chessboard is: $\frac{1}{R_{eq}} = \frac{1}{R_{row}} + \frac{1}{R_{row}} + \dots \text{(8 times)}$ $\frac{1}{R_{eq}} = \frac{8}{R_{row}}$ $R_{eq} = \frac{R_{row}}{8}$ Substitute the expression for $R_{row}$: $R_{eq} = \frac{1}{8} \left[ \frac{4}{t} \left( \frac{\sigma_1 + \sigma_2}{\sigma_1 \sigma_2} \right) \right]$ $R_{eq} = \frac{1}{2t} \left( \frac{\sigma_1 + \sigma_2}{\sigma_1 \sigma_2} \right)$

5. Current flowing through the chessboard:

   Using Ohm's Law, $I = \frac{V}{R_{eq}}$: $I = \frac{V}{\frac{1}{2t} \left( \frac{\sigma_1 + \sigma_2}{\sigma_1 \sigma_2} \right)}$ $I = V \frac{2t \sigma_1 \sigma_2}{\sigma_1 + \sigma_2}$

The current flowing through the chessboard is $V \frac{2t \sigma_1 \sigma_2}{\sigma_1 + \sigma_2}$.