Solveeit Logo
Login

Question

Question: P-V diagram of an ideal gas is shown in figure. Work done by the gas in the process ABCD is- ![...

P-V diagram of an ideal gas is shown in figure. Work done by the gas in the process ABCD is-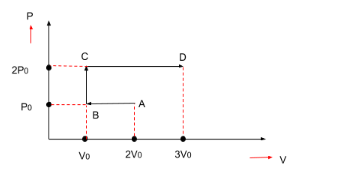

A.)2P0V02{P_0}{V_0}
B.)3P0V03{P_0}{V_0}
C.)P0V0{P_0}{V_0}
D.)4P0V04{P_0}{V_0}

Explanation

Solution

Hint: We will find out the work done from point A to point B. from point B to point C, from point C to point D respectively. Then we will add the values of each work done in order to find out the total work done. Refer to the solution below.
Formula used: WAB=P×ΔV=area{W_{AB}} = P \times \Delta V = area

Complete answer:
As we know that the work done for the P-V curve is the area under the P-V curve.
First, we will find out the work done from point A to point B.

⇒WAB=P×ΔV=area \Rightarrow {W_{AB}} = P \times \Delta V = area (as shown in the figure)
Pressure = P0{P_0}

Volume-

Initial volume is 2V02{V_0}
Final volume is V0{V_0}
⇒V0−2V0=−V0\Rightarrow {V_0} - 2{V_0} = - {V_0}

Substituting these values in the formula for work done-

⇒WAB=P×ΔV  ⇒WAB=−P0(V0)  ⇒WAB=−P0V0  \Rightarrow {W_{AB}} = P \times \Delta V \\\ \\\ \Rightarrow {W_{AB}} = - {P_0}\left( {{V_0}} \right) \\\ \\\ \Rightarrow {W_{AB}} = - {P_0}{V_0} \\\

Now, we will find out the work done from point B to point C.
⇒WBC=P×ΔV=area\Rightarrow {W_{BC}} = P \times \Delta V = area (as shown in the figure)

Volume in this case will be as zero as can be seen from the figure. Hence, the work done will also be zero.

⇒WBC=0 \Rightarrow {W_{BC}} = 0
Now, we will find out the work done from point C to point D.
⇒WCD=P×ΔV=area\Rightarrow {W_{CD}} = P \times \Delta V = area (as shown in the figure)
Pressure = 2P02{P_0}

Volume-

Initial volume is V0{V_0}
Final volume is 3V03{V_0}
⇒3V0−V0=2V0\Rightarrow 3{V_0} - {V_0} = 2{V_0}

Substituting these values in the formula for work done-

⇒WAB=P×ΔV  ⇒WAB=2P0(2V0)  ⇒WAB=4P0V0  \Rightarrow {W_{AB}} = P \times \Delta V \\\ \\\ \Rightarrow {W_{AB}} = 2{P_0}\left( {2{V_0}} \right) \\\ \\\ \Rightarrow {W_{AB}} = 4{P_0}{V_0} \\\

Now, work done in total will be the sum of all the above values-

⇒WT=−P0V0+0+4P0V0  ⇒WT=3P0V0  \Rightarrow {W_T} = - {P_0}{V_0} + 0 + 4{P_0}{V_0} \\\ \\\ \Rightarrow {W_T} = 3{P_0}{V_0} \\\

Hence, it is clear that option B is the correct option.

Note: Gas can work against excessive ambient pressure by extending or compressing it. Work done is often referred to as the amount of pressure-volume or PV. The volume of a gas increases