Question

P' speaks the truth 5 out of 12 times and 'Q' speaks the truth 8 out of 21 times. What is the probability that they contradict each other in stating the same fact?

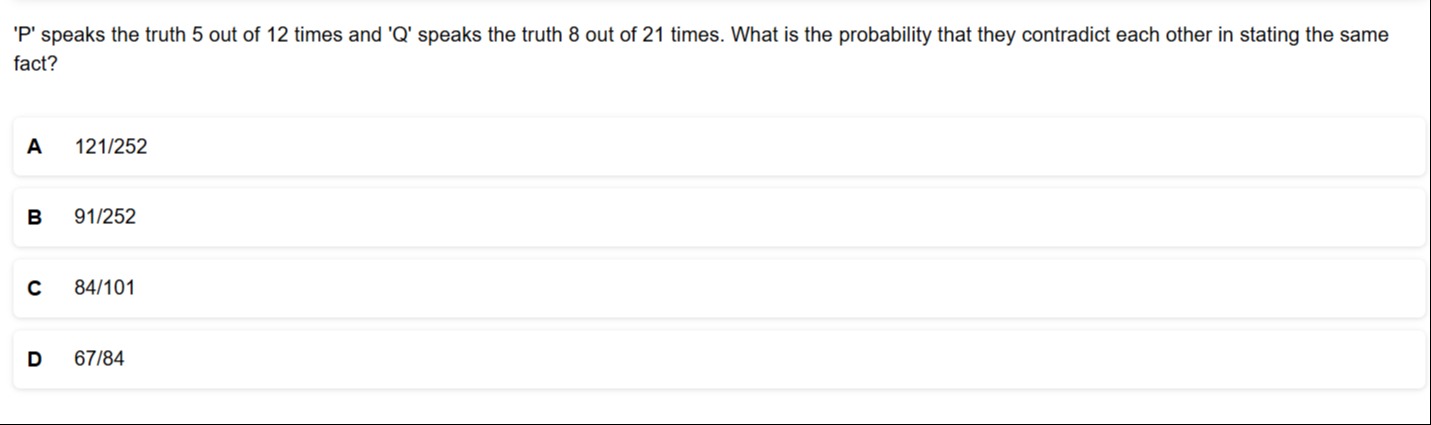
• A. 121/252
• B. 91/252
• C. 84/101
• D. 67/84

Answer 1

Answer: (A)

121/252

Answer 2

To find the probability that P and Q contradict each other, we consider two scenarios:

1. P speaks the truth and Q speaks a lie.
2. P speaks a lie and Q speaks the truth.

Let $P(P_T)$ be the probability that P speaks the truth.
Let $P(Q_T)$ be the probability that Q speaks the truth.

Given:
$P(P_T) = \frac{5}{12}$
$P(Q_T) = \frac{8}{21}$

The probability that P speaks a lie, $P(P_L)$, is $1 - P(P_T)$.
$P(P_L) = 1 - \frac{5}{12} = \frac{12 - 5}{12} = \frac{7}{12}$

The probability that Q speaks a lie, $P(Q_L)$, is $1 - P(Q_T)$.
$P(Q_L) = 1 - \frac{8}{21} = \frac{21 - 8}{21} = \frac{13}{21}$

For them to contradict each other, one must speak the truth and the other must speak a lie. Since their statements are independent events, we can multiply their probabilities.

Scenario 1: P speaks the truth AND Q speaks a lie.
Probability = $P(P_T) \times P(Q_L) = \frac{5}{12} \times \frac{13}{21} = \frac{65}{252}$

Scenario 2: P speaks a lie AND Q speaks the truth.
Probability = $P(P_L) \times P(Q_T) = \frac{7}{12} \times \frac{8}{21} = \frac{56}{252}$

The total probability that they contradict each other is the sum of the probabilities of these two mutually exclusive scenarios:
$P(\text{contradiction}) = P(P_T) \times P(Q_L) + P(P_L) \times P(Q_T)$
$P(\text{contradiction}) = \frac{65}{252} + \frac{56}{252}$
$P(\text{contradiction}) = \frac{65 + 56}{252} = \frac{121}{252}$