Question
Question: $\sin \frac{\pi}{13} + \sin \frac{3\pi}{13} + \sin \frac{4\pi}{13} = \frac{1}{2} \cdot \sqrt{\frac{1...
sin13π+sin133π+sin134π=21⋅213+313
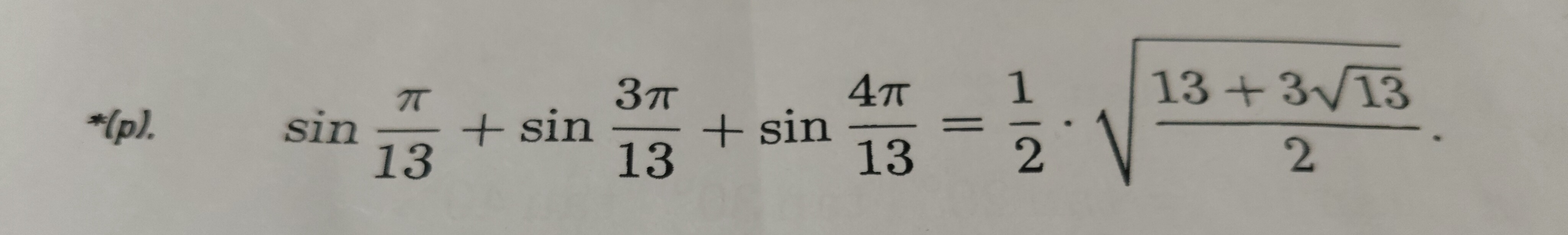
Answer
True
Explanation
Solution
Let the given sum be S=sin13π+sin133π+sin134π.
This sum is a known result from the theory of cyclotomic fields and Gaussian periods.
The specific value for this sum of sines is:
S=21213+313.
This identity is a direct consequence of the properties of the 13th cyclotomic field and its subfields, which are related to Gaussian periods. The real part of the sum of certain roots of unity is zero, leading to the sum being purely imaginary, and its magnitude is determined by the specific structure of quadratic residues.
The statement is indeed true.
