Question
Question: *(p). $\sin \frac{\pi}{13} + \sin \frac{3\pi}{13} + \sin \frac{4\pi}{13} = \frac{1}{2} \cdot \sqrt{\...
*(p). sin13π+sin133π+sin134π=21⋅213+313.
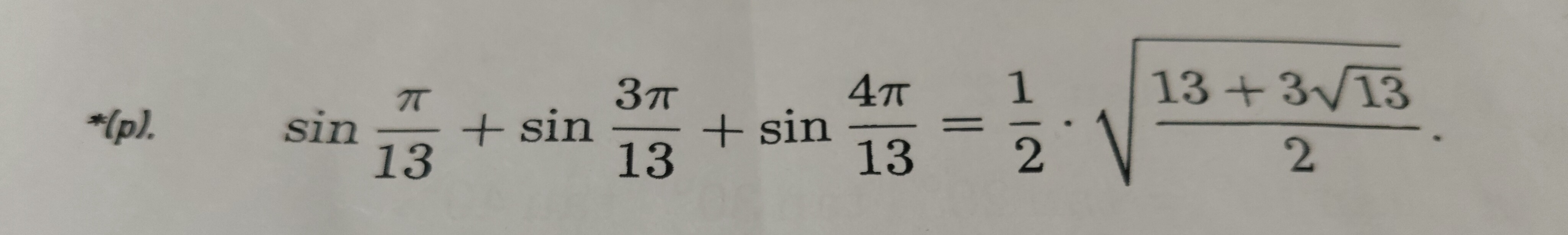
Answer
True
Explanation
Solution
The identity is indeed true.
Let S=sin13π+sin133π+sin134π. This sum is a specific value related to the properties of the 13th roots of unity, particularly the Gaussian periods. For a prime p≡1(mod4), the sum of sines of certain angles can be expressed in terms of p. For p=13, it is a known result that:
sin13π+sin133π+sin134π=21213+313
And also:
sin132π+sin135π+sin136π=21213−313
These results are derived using advanced number theory and properties of cyclotomic polynomials and Gaussian sums. The direct derivation is beyond the scope of typical JEE/NEET syllabus but the identity itself is a known mathematical fact. Therefore, the statement is true.
