Question

P, Q and R represent switches in on position and P’, Q’ and R’ represent switches in off position. Construct a switching circuit representing the polynomial PR + Q(Q’ + R)(P + QR). Using Boolean algebra, simplify the polynomial expression and construct the simplified circuit.

Answer 1

Hint:We will use the axioms of Boolean algebra. Here we will use two out of all the axioms, which are given by a.a’ = 0 and the other one as a.(a + b) = 0.

Complete step-by-step answer:

We will first discuss Boolean algebra in order to solve the equation PR + Q(Q’ + R)(P + QR). So, any algebraic system of a set B with elements a, b, c, …… along with two basic binary operations namely represented as + and product denoted by . (dot). To prove it as a Boolean algebra, we are supposed to prove the following axioms, and then the algebraic system will be equal to the concept of Boolean algebra. The axioms are,
(i) $a+b\in R$ and $a.b\in R,\forall a,b\in B$. Here B is any set in algebraic system. This axiom is the closure property.
(ii) $a+b=b+a$ and $a.b=b.a$. This proves the communicative property with first expression with respect to sum and second expression with respect to product. This is $\forall a,b\in B$.
(iii) $\left( a+b \right)+c=a+\left( b+c \right)$. This is the associative law with respect to addition and, $\left( a.b \right).c=a.\left( b.c \right)$ with respect to multiplication. This is $\forall a,b,c\in B$.
(iv) $a.\left( b+c \right)=a.b+a.c,\forall a,b,c\in B$. This satisfies the distributive law under which addition and $\forall a,b,c\in B$ the term $a+\left( b.c \right)=\left( a+b \right).\left( a+c \right)$ satisfies right distributive law.
(v) For each $a\in B$ is an additive identity in B such that $a+\left( -a \right)=0$ or $a+0=a$ also for each $a\in B$ is an inverse or multiplicative identity in B such that $a.{{a}^{-1}}=1$ or $a.1=a$.
(vi) For each $a\in B$ is an element $a'\in B$ called as a complement or an inverse, such that $a+a'=1$ or $a.a'=0$.
Now we will consider the equation or the polynomial as, PR + Q(Q’ + R)(P + QR)…… (vii).
The question clearly states that P, Q and R represent switches in on position and P’, Q’ and R’ represent switches in off position. In case of switches, we will consider multiplication for switches that are in series and when we are given addition, then the switches are in parallel concept. Now we will consider the equation (vii) and draw a circuit for it. We need to remember that PR are in multiplication, which means that the switches P and R are in series. Q’ + R, represents that Q’ is in off position and Q’ and R are in parallel format. And P +QR means that the switches Q and R are in series and P is parallel with respect to QR. Q and (Q’ + R) are also in series along with P + QR, which are also in series. So, as a whole, PR is parallel with respect to Q(Q’ + R)(P + QR). So, the diagram for the polynomial, PR + Q(Q’ + R)(P + QR) will be given as follows,

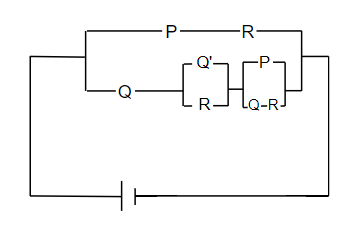
Now, we will again consider equation (vii), PR + Q(Q’ + R)(P + QR). Multiplying Q to (Q’ + R), we get PR + (QQ’ + QR)(P + QR). By applying axiom (vi) we get QQ’ = 0. We have used the axiom as this polynomial is a Boolean polynomial, and it will satisfy all the axioms of Boolean algebra. So, we get, PR + (QQ’ +QR)(P + QR) = PR +QR(P + QR)……(viii)
Now, here we have a proof which states that a.(a + b) = a. So, if we consider the left hand side a.(a + b), it results in (a +0)(a + b). This is because a = a + 0 as 0 is an additive identity satisfying it. Now, by applying axiom (vi) here, we get a new equation as, (a +0)(a + b) = a + (0.b). We know that 0.b = 0, thus we have a + 0 = a. Now, we apply the proof of a.(a + b) = a in equation (viii), therefore we get, PR +QR(P + QR) = PR + QR.
Hence, we have reached a simpler circuit diagram, which can be represented as,

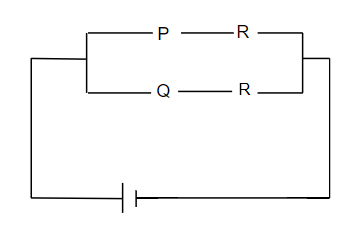
Note: This circuit clearly explains that since P and R are in series, then the switch will be on if both P and R are on. Similarly, if both Q and R are on, then the light will be on. But only one of the pairs out of P-R and Q-R should work in order to switch on the light. Alternatively, this Boolean algebra of equation (vii) could have also been simplified one step further and resulted in (P + Q)R. When we applied the axiom a.(a + b) = a, we could have also proved it by duality, which implies that a +a.b = a.