Question

P $\left( -1,4 \right)$, Q $\left( 11,-8 \right)$ divides AB harmonically in the ratio $3:2$ then A,B are?

Answer 1

Using the section formula method we first multiply the $x$ coordinates with the ratio $3:2$ and then do the same for $y$ coordinates as well.
For $x$ coordinates and coordinates of A and B as $\left( a,b \right)$ and $\left( x,y \right)$ with ratio
$\left( m:n \right)$:
$\dfrac{mx+na}{m+n}$
For $y$ coordinates and coordinates of A and B as $\left( a,b \right)$ and $\left( x,y \right)$ with ratio$\left( m:n \right)$:
$\dfrac{my+nb}{m+n}$
The previous formula was applied for P coordinate and now we will do the same for Q coordinates as well. The ratio of $3:2$ will change to $-3:2$ as Q is a harmonic conjugate of P.

Complete step by step solution:
Now as given in the question, we first form a coordinate diagram where P is the midpoint with A, B as extreme and the distance of AP is 3 and the distance of PB is 2.

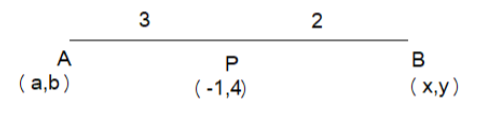
After this let us form an equation with the help of A's coordinate and B's coordinate with midpoint as
$\left( -1,4 \right)$.
The equation for the $a$ or $x$ coordinate is given as:
$\Rightarrow \dfrac{3\times x+2\times a}{3+2}=-1$
$\Rightarrow 3x+2a=-5$ …(1)
The equation for the $b$ or $y$ coordinate is given as:
$\Rightarrow \dfrac{3\times y+2\times b}{3+2}=4$
$\Rightarrow 3y+2b=20$ …(2)
We now find equation for $x$ and $y$ with midpoint being $\left( 11,-8 \right)$ and the ratio of distance from AQ to QB as $\left( -3:2 \right)$ as Q is harmonic conjugate of P.
The equation for the $a$ or $x$ coordinate is given as:
$\Rightarrow \dfrac{-3\times x+2\times a}{-3+2}=11$
$\Rightarrow -3x+2a=-11$ …(3)
The equation for the $b$ or $y$ coordinate is given as:
$\Rightarrow \dfrac{-3\times y+2\times b}{-3+2}=8$
$\Rightarrow -3y+2b=8$ …(4)
Now we equate the Equation 1, 2, 3 and 4; So as to find the value of a, b. First we find for the value of a by equating equation 1,3.

& \text{ }3x+2a=-5 \\\ & -3x+2a=-11 \\\ & \text{ +}4a=-16 \\\ \end{aligned}$$ $$\Rightarrow a=-4$$ We get the value of $$a$$ as $$-4$$ and to find the value of $$x$$ we place the value of $$a$$ in $$3x+2a= -5$$. $$\Rightarrow 3x+2\times -4=-5$$ $$\Rightarrow 3x=8-5$$ $$\Rightarrow x=1$$ Then we find for the value of b by Equating equation 2,4. $$\begin{aligned} & \text{ }3y+2b=20 \\\ & -3y+2b=8 \\\ & \text{ +}4b=28 \\\ \end{aligned}$$ $$\Rightarrow b=7$$ We get the value of $$b$$ as $$7$$ and to find the value of $$x$$ we place the value of $$b$$ in $$-3y+2b=8$$. $$\Rightarrow -3y+2\times 7=8$$ $$\Rightarrow -3y=-14+8$$ $$\Rightarrow y=2$$ **Therefore, the value of a, b or A, B is given as $$\left( -4:7 \right)$$** **Note:** The term harmonic conjugate means that if the line is divided let say in ratio of $$\text{AC:BC = AD:BD}$$ we can say that C and D are cutting the line AB harmonically and that AB and CD are harmonic conjugates.