Solveeit Logo
Login

Question

Question: P is the mid-point of the line segment AB. The coordinates of P are (5,-6). The coordinates of A are...

P is the mid-point of the line segment AB. The coordinates of P are (5,-6). The coordinates of A are (-1,10). How do you find the coordinate of B?

Explanation

Solution

No matter whether the line is in 2d, 3d or 4d space the midpoint of a line segment is always equal to the sum of the coordinates divided by two. Since in this problem we are given the midpoint of the line segment and coordinate of one of the endpoints we can use the other mid-point as a variable and get the it's by using the midpoint formula.

Midpoint formula:
Mid-point=((x1+x22),(y1+y22)) = \left( {\left( {\dfrac{{{x_1} + {x_2}}}{2}} \right),\left( {\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right)
Where the coordinates of the points are (x1,y1)\left( {{x_1},{y_1}} \right) and (x2,y2)\left( {{x_2},{y_2}} \right)

Complete step-by-step answer:
If two coordinates are given, we know the formula for finding the midpoint is:
Mid-point=((x1+x22),(y1+y22)) = \left( {\left( {\dfrac{{{x_1} + {x_2}}}{2}} \right),\left( {\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right); formula
Where the coordinates of the points are (x1,y1)\left( {{x_1},{y_1}} \right) and (x2,y2)\left( {{x_2},{y_2}} \right)
Now in the question coordinate of one of the points and the coordinate of the midpoint is given to us
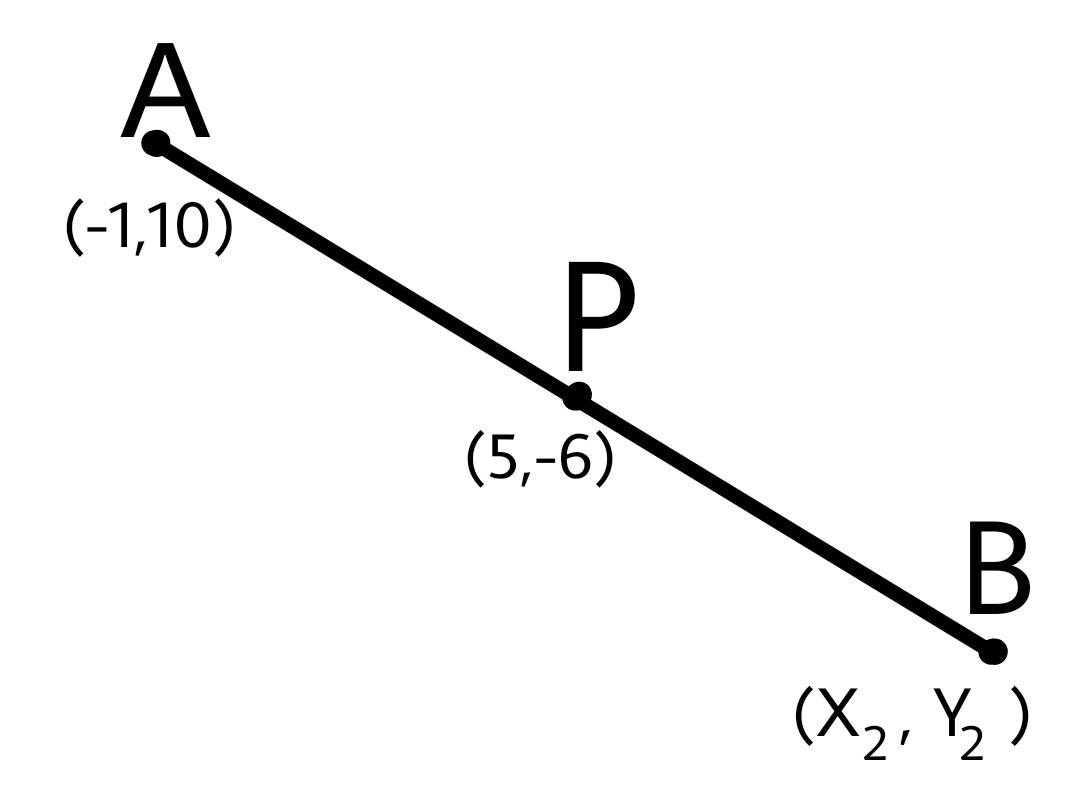
In the given figure mid-point of the line AB is P=(5,−6)P = \left( {5, - 6} \right) and A=(−1,10)A = \left( { - 1,10} \right)

Now we need to find the coordinate of B
We will substitute the values of P as the mid-point and A as the first coordinate in the formula of midpoint
(5,−6)=((−1+x22),(10+y22))\left( {5, - 6} \right) = \left( {\left( {\dfrac{{ - 1 + {x_2}}}{2}} \right),\left( {\dfrac{{10 + {y_2}}}{2}} \right)} \right)
To get values of(x2,y2)\left( {{x_2},{y_2}} \right)is by equating the x-coordinate with 5 and equating the y-coordinate with -6
Let’s find X-coordinate:
(−1+x22)=5\left( {\dfrac{{ - 1 + {x_2}}}{2}} \right) = 5
−1+x2=5×2- 1 + {x_2} = 5 \times 2
x2=10+1{x_2} = 10 + 1
x2=11{x_2} = 11
Let’s find the Y-coordinate:
10+y22=−6\dfrac{{10 + {y_2}}}{2} = - 6
10+y2=−6×210 + {y_2} = - 6 \times 2
y2=−12−10{y_2} = - 12 - 10
y2=−22{y_2} = - 22
So the coordinates of B=(11,−22)B = \left( {11, - 22} \right)

Note: Try to be very careful with the negative signs of the coordinates this is where most people go wrong. And when finding the midpoint when both the points are given directly apply the midpoint formula. A line segment which is in the third dimensional plane has three coordinates of its midpoint so when we are solving for the coordinates we will get three different equations, and the same four different equations for the fourth dimensional plane.