Question
Question: f(x) = x - \sqrt{x^2 - 1}...
f(x) = x - \sqrt{x^2 - 1}
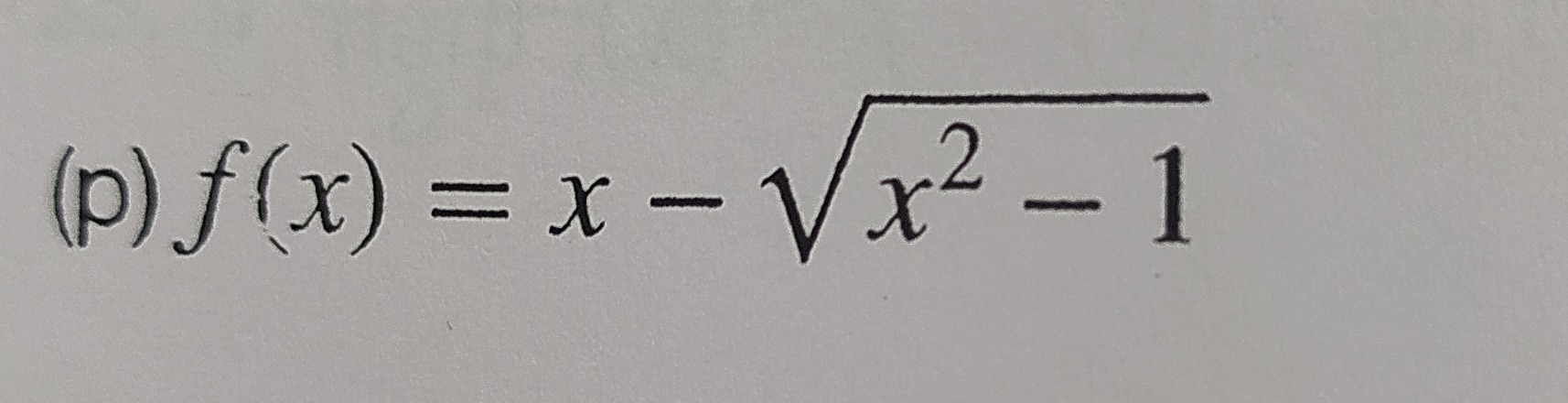
-
Domain: (−∞,−1]∪[1,∞)
-
Range: (−∞,−1]∪(0,1]
-
Inverse function: f−1(x)=2xx2+1 for x∈(−∞,−1]∪(0,1].
Solution
The function given is f(x)=x−x2−1.
-
Domain: The term x2−1 requires x2−1≥0, which means (x−1)(x+1)≥0. This inequality holds for x≤−1 or x≥1. The domain of f(x) is D=(−∞,−1]∪[1,∞).
-
Range:
-
Consider x≥1. We can rewrite f(x) by multiplying by the conjugate: f(x)=(x−x2−1)x+x2−1x+x2−1=x+x2−1x2−(x2−1)=x+x2−11. For x≥1, x is positive and x2−1≥0. Thus, x+x2−1 is positive. As x→∞, x+x2−1→∞, so limx→∞f(x)=limx→∞x+x2−11=0. At x=1, f(1)=1−12−1=1. The derivative f′(x)=1−x2−1x for x>1. Since x2−1x=x2−1x2=1+x2−11>1 for x>1, f′(x)<0. The function is decreasing on [1,∞). The range for x∈[1,∞) is (0,1].
-
Consider x≤−1. Let x=−y where y≥1. f(x)=f(−y)=−y−(−y)2−1=−y−y2−1. As y→∞ (i.e., x→−∞), −y→−∞ and −y2−1→−∞. So, limx→−∞f(x)=−∞. At x=−1, f(−1)=−1−(−1)2−1=−1. The derivative f′(x)=1−x2−1x for x<−1. Let x=−y with y>1. f′(x)=1−(−y)2−1−y=1+y2−1y. For y>1, y2−1y>0, so f′(x)>1>0. The function is increasing on (−∞,−1]. The range for x∈(−∞,−1] is (−∞,−1].
The total range of f(x) is the union of the ranges from the two intervals: R=(−∞,−1]∪(0,1].
-
-
Injectivity: The function is strictly increasing on (−∞,−1] and strictly decreasing on [1,∞). Also, the ranges for these two intervals, (−∞,−1] and (0,1], are disjoint. This means that any value in the range is attained for a unique value of x in the domain. Therefore, the function f(x) is injective (one-to-one) on its domain.
-
Inverse Function: Since f(x) is injective, its inverse f−1(x) exists. Let y=x−x2−1. We want to solve for x in terms of y. y−x=−x2−1 x−y=x2−1 Squaring both sides: (x−y)2=x2−1 x2−2xy+y2=x2−1 −2xy+y2=−1 2xy=y2+1 x=2yy2+1. Thus, the inverse function is f−1(y)=2yy2+1. Replacing y with x, we get f−1(x)=2xx2+1. The domain of f−1(x) is the range of f(x), which is (−∞,−1]∪(0,1]. The range of f−1(x) is the domain of f(x), which is (−∞,−1]∪[1,∞).
Summary of properties:
- Domain: (−∞,−1]∪[1,∞)
- Range: (−∞,−1]∪(0,1]
- Monotonicity: Increasing on (−∞,−1], Decreasing on [1,∞)
- Injectivity: Injective
- Inverse function: f−1(x)=2xx2+1 with domain (−∞,−1]∪(0,1].
