Question

P and Q are two points with the position vectors $3\overset{\to }{\mathop{a}}\,-2\overset{\to }{\mathop{b}}\,$ and $\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,$ respectively. Write the position vector of a point R which divides the line segment PQ in the ratio $2:1$ externally.

Answer 1

Let us assume that for given two position vectors and We have two position vectors as: $\overset{\to }{\mathop{OP}}\,=3\overset{\to }{\mathop{a}}\,-2\overset{\to }{\mathop{b}}\,$ and $\overset{\to }{\mathop{OQ}}\,=\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,$. It is also given that a position vector $\overset{\to }{\mathop{OR}}\,$divides the line segment PQ externally in ratio $2:1$. So, we need to find $\overset{\to }{\mathop{OR}}\,$.

Complete step-by-step solution:
By using the section formula for external division, i.e. $\overset{\to }{\mathop{r}}\,=\dfrac{m\times \overset{\to }{\mathop{b}}\,-n\times \overset{\to }{\mathop{a}}\,}{m-n}$, find the coordinates of vector $\overset{\to }{\mathop{OR}}\,$, i.e. position vector of point R.

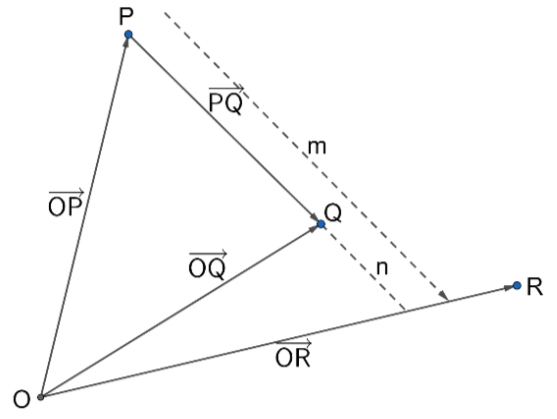
From the above diagram, we have two points P and Q whose position vectors are $3\overset{\to }{\mathop{a}}\,-2\overset{\to }{\mathop{b}}\,$ and $\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,$ respectively. So, we get two vectors as:
$\overset{\to }{\mathop{OP}}\,=3\overset{\to }{\mathop{a}}\,-2\overset{\to }{\mathop{b}}\,......(1)$
$\overset{\to }{\mathop{OQ}}\,=\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,......(2)$
Since it is given that position vector of point R, i.e. $\overset{\to }{\mathop{OR}}\,$ divides the line segment in ratio $2:1$ externally.
So, by using section formula for external division $\overset{\to }{\mathop{r}}\,=\dfrac{m\times \overset{\to }{\mathop{b}}\,-n\times \overset{\to }{\mathop{a}}\,}{m-n}$ for vector $\overset{\to }{\mathop{OR}}\,$, we get:
$\overset{\to }{\mathop{OR}}\,=\dfrac{2\times \overset{\to }{\mathop{OQ}}\,-1\times \overset{\to }{\mathop{OP}}\,}{2-1}......(3)$
Put the values of equation (1) and (2) in equation (3), we get:

& \overset{\to }{\mathop{OR}}\,=\dfrac{2\times \left( \overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\, \right)-1\times \left( \overset{\to }{\mathop{3a}}\,-2\overset{\to }{\mathop{b}}\, \right)}{2-1} \\\ & =2\overset{\to }{\mathop{a}}\,+2\overset{\to }{\mathop{b}}\,-3\overset{\to }{\mathop{a}}\,+2\overset{\to }{\mathop{b}}\, \\\ & =-\overset{\to }{\mathop{a}}\,+4\overset{\to }{\mathop{b}}\, \end{aligned}$$ **Hence, position vector of point R is $-\overset{\to }{\mathop{a}}\,+4\overset{\to }{\mathop{b}}\,$** **Note:** As it is mentioned in the question that the position vector of R divides line segment PQ externally, so we need to apply section formula for external division. Students might use the section formula for internal division, i.e. $\overset{\to }{\mathop{r}}\,=\dfrac{m\times \overset{\to }{\mathop{b}}\,+n\times \overset{\to }{\mathop{a}}\,}{m+n}$ instead of section formula for external division, i.e. $\overset{\to }{\mathop{r}}\,=\dfrac{m\times \overset{\to }{\mathop{b}}\,-n\times \overset{\to }{\mathop{a}}\,}{m-n}$. Also, while drawing the diagram of the vectors, the position vector of R does not intersect the line segment PQ. But it lies external to the line segment PQ as shown in the diagram above.