Question

A B

Answer 1

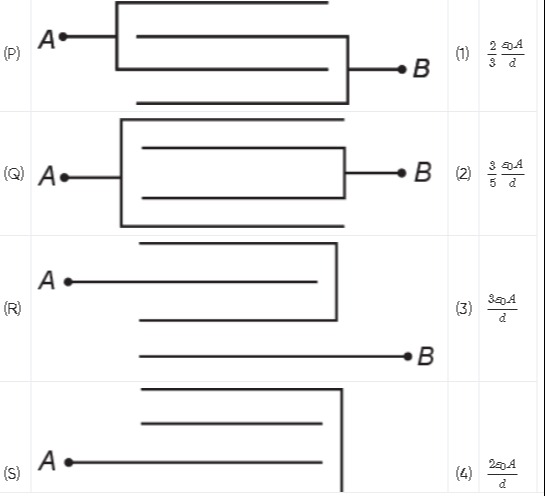
Configuration (P) matches option (4), Configuration (Q) matches option (3), Configuration (R) matches option (3). The diagram for (S) does not show a connection to terminal B. Without terminal B, the capacitance between A and B cannot be determined. Therefore, this part of the question is ambiguous or incomplete as presented.

Answer 2

Configuration (P)

The configuration consists of 3 plates.

• The top plate is connected to terminal A.

• The middle plate is connected to terminal B.

• The bottom plate is connected to terminal A.

This arrangement forms two parallel plate capacitors:

1. Between the top plate (A) and the middle plate (B). Its capacitance is $C_0$.

2. Between the middle plate (B) and the bottom plate (A). Its capacitance is $C_0$.

Since both capacitors are connected between the same two terminals (A and B), they are in parallel. The equivalent capacitance $C_P = C_0 + C_0 = 2C_0 = \frac{2\epsilon_0 A}{d}$.

This matches option (4).

Configuration (Q)

The configuration consists of 4 plates.

• Plate 1 (from top) is connected to A.

• Plate 2 is connected to B.

• Plate 3 is connected to A.

• Plate 4 is connected to B.

This arrangement forms three parallel plate capacitors:

1. Between Plate 1 (A) and Plate 2 (B). Its capacitance is $C_0$.

2. Between Plate 2 (B) and Plate 3 (A). Its capacitance is $C_0$.

3. Between Plate 3 (A) and Plate 4 (B). Its capacitance is $C_0$.

All three capacitors are connected between terminals A and B, so they are in parallel. The equivalent capacitance $C_Q = C_0 + C_0 + C_0 = 3C_0 = \frac{3\epsilon_0 A}{d}$.

This matches option (3).

Configuration (R)

The configuration consists of 5 plates.

• Plate 1 (from top) is connected to A.

• Plate 2 is connected to A.

• Plate 3 is connected to B.

• Plate 4 is connected to A.

• Plate 5 is connected to B.

Let's identify the capacitors formed:

• Between Plate 1 (A) and Plate 2 (A): No capacitor is formed as both plates are at the same potential.

• Between Plate 2 (A) and Plate 3 (B): This forms a capacitor with capacitance $C_0$.

• Between Plate 3 (B) and Plate 4 (A): This forms a capacitor with capacitance $C_0$.

• Between Plate 4 (A) and Plate 5 (B): This forms a capacitor with capacitance $C_0$.

The three active capacitors are all connected between terminals A and B, so they are in parallel. The equivalent capacitance $C_R = C_0 + C_0 + C_0 = 3C_0 = \frac{3\epsilon_0 A}{d}$.

This matches option (3).

Configuration (S)

The configuration consists of 4 plates.

• Plate 1 (from top) is connected to A.

• Plate 2 is isolated (floating).

• Plate 3 is connected to A.

• Plate 4 is isolated (floating).

The diagram for (S) does not show any connection to terminal B. Without a second terminal (B), or any other specified reference point, it is not possible to determine the capacitance of this configuration between A and B. Therefore, this part of the question is ambiguous or incomplete as presented.

Based on the clear matches:

(P) $\rightarrow$ (4)

(Q) $\rightarrow$ (3)

(R) $\rightarrow$ (3)

The question is a match-the-column type.

The final answer is $\boxed{(P) \rightarrow (4), (Q) \rightarrow (3), (R) \rightarrow (3)}$

Explanation of the solution:

1. Identify individual capacitors: For each pair of adjacent plates connected to different terminals (A and B), a capacitor of capacitance $C_0 = \frac{\epsilon_0 A}{d}$ is formed. If adjacent plates are connected to the same terminal, no capacitor is formed between them.

2. Determine connection type: If multiple capacitors are formed, check if they are connected between the same two main terminals (A and B). If so, they are in parallel. If they are connected end-to-end such that the charge on one is equal to the charge on the next, they are in series.

3. Calculate equivalent capacitance:

   • For parallel capacitors: $C_{eq} = C_1 + C_2 + ...$

   • For series capacitors: $\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ...$

Applying this:

• (P) has 3 plates (A-B-A). Two $C_0$ capacitors in parallel. $C_P = 2C_0$.

• (Q) has 4 plates (A-B-A-B). Three $C_0$ capacitors in parallel. $C_Q = 3C_0$.

• (R) has 5 plates (A-A-B-A-B). One (A-A) pair forms no capacitor. Three $C_0$ capacitors remain, in parallel. $C_R = 3C_0$.

• (S) has an incomplete diagram, lacking a connection to terminal B, making its capacitance indeterminable as presented.

Answer:

The matches are:

(P) $\rightarrow$ (4)

(Q) $\rightarrow$ (3)

(R) $\rightarrow$ (3)

(Note: Configuration (S) is incomplete as no connection to terminal B is shown, making it impossible to determine its capacitance between A and B.)