Question

P(2, k) and Q(2, -k) are the points of the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{4} = 1$.

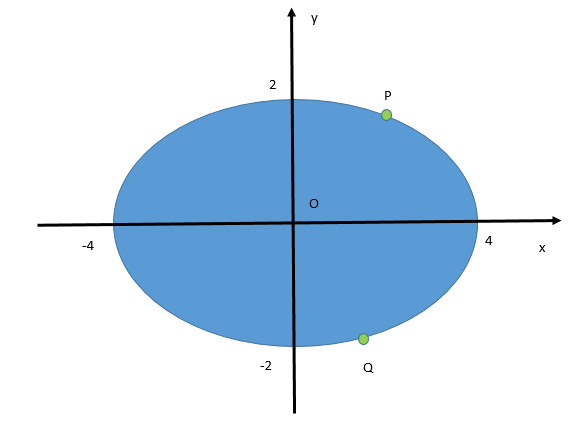
Find the value of k.

Answer 1

We will put in the coordinates of the points P and Q in the equation of the ellipse given to us component wise and thus, we will obtain an equation in k which will give us the answer.

Complete step by step answer:
Since, we are given that P (2, k) and Q (2, -k) pass through the ellipse. Hence, they must satisfy the equation of the ellipse.
Now, we will put in the coordinates of P that is (2, k) in the given equation of the ellipse which is $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{4} = 1$.
So, putting in x = 2 and y = k, we will then get the following expression:-
$\Rightarrow \dfrac{{{2^2}}}{{16}} + \dfrac{{{k^2}}}{4} = 1$
Simplifying the square value of LHS, we will then obtain:-
$\Rightarrow \dfrac{4}{{16}} + \dfrac{{{k^2}}}{4} = 1$
Simplifying the LHS again, we will get:-
$\Rightarrow \dfrac{1}{4} + \dfrac{{{k^2}}}{4} = 1$
Taking $\dfrac{1}{4}$ from addition in LHS to subtraction in RHS, we will then obtain:-
$\Rightarrow \dfrac{{{k^2}}}{4} = 1 - \dfrac{1}{4}$
Taking LCM on RHS, we will get:-
$\Rightarrow \dfrac{{{k^2}}}{4} = \dfrac{{4 - 1}}{4}$
We can write it as:
$\Rightarrow \dfrac{{{k^2}}}{4} = \dfrac{3}{4}$
Cutting off 4 from denominators of both LHS and RHS, we will get:-
$\Rightarrow {k^2} = 3$
Taking square root on both the sides, we will get:
$\Rightarrow k = \pm \sqrt 3$.

$\therefore$ The value of k is $\pm \sqrt 3$.

Note:
The students must note that we did cut off 4 from the denominator in one step, we can just do it with non-zero quantities. So, if there is any variable in denominators, you can cut it off only when you rule out the possibility of that being equal to zero anytime. Since, 4 can never be equal to 0, therefore, we could easily remove it.
The students might also wonder that, we used only one of the points among P and Q, we did that because we just had one unknown variable k and that can be done with only one equation. There is one more reason for that as well. Even if you put another point, it will give the same equation because the y component which is different in those points is getting squared and thus resulting in the same equation.