Question

Oxidation number of Cr in $Cr{O_5}$ is:

$A) + 10 \\\ B) + 6 \\\ C) + 4 \\\ D) + 5 \\\$

Answer 1

We can define oxidation state as oxidation degree (loss of an electron) in a chemical compound. We can calculate the oxidation state by an element in a compound by using the rules of oxidation numbers.

Complete step by step answer:
We know that oxidation state is the loss of an electron in a chemical compound. We can now see a few rules of oxidation numbers.

-A free element will be zero as its oxidation number.
-Monatomic ions will have an oxidation number equal to charge of the ion.
-In hydrogen, the oxidation number is ${\text{ + 1,}}$ when combined with elements having less electronegativity, the oxidation number of hydrogen is -1.
-In compounds of oxygen, the oxidation number of oxygen will be -2 and in peroxides, it will be -1.
-Group 1 elements will have +1 oxidation number.
-Group 2 elements will have +2 oxidation numbers.
-Group 17 elements will have -1 oxidation number.
-Sum of oxidation numbers of all atoms in neutral compounds is zero.
-In polyatomic ions, the sum of the oxidation number is equal to the ionic charge.

We can draw the structure of $Cr{O_5}$ as,

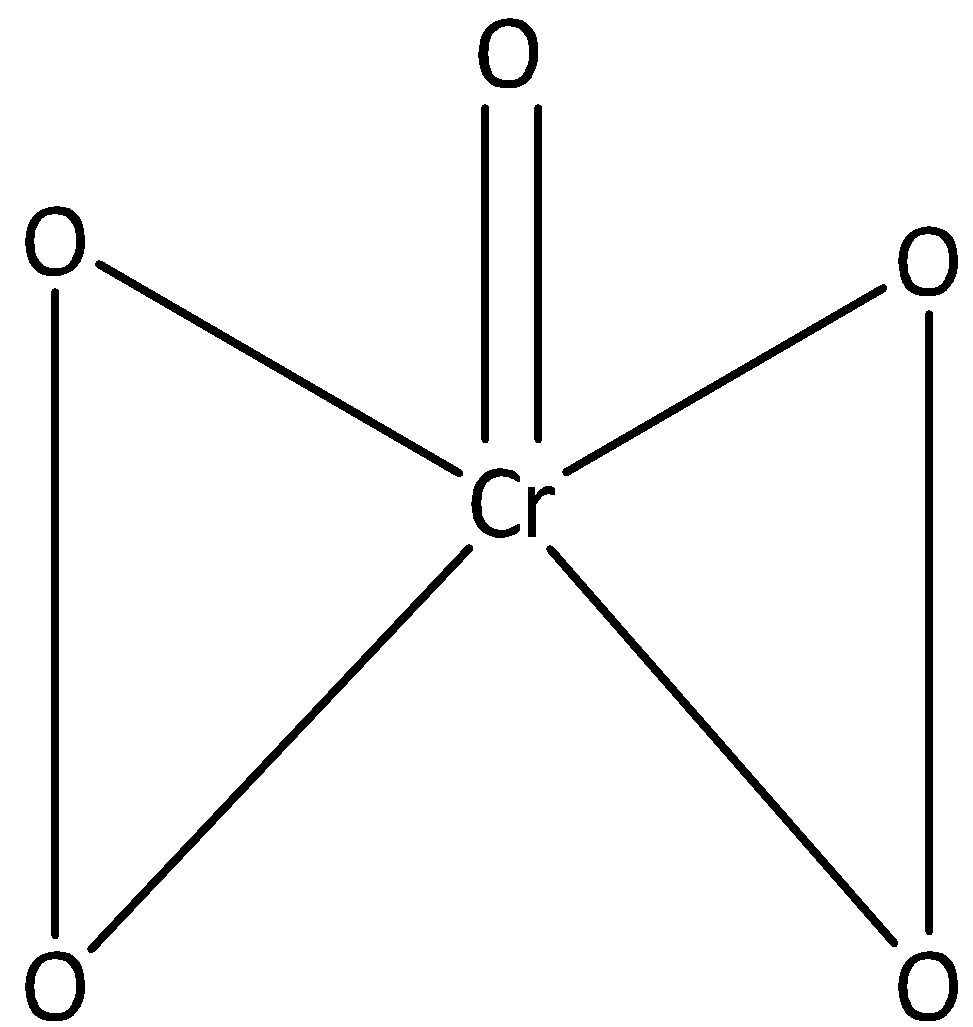
In $Cr{O_5}$ one atom of oxygen is linked to chromium through the double bond, and the oxidation number is -2. The remaining four oxygen atoms are linked to chromium through a single bond, and their oxidation number is -1.

Let us now calculate the oxidation state of Cr in ${\text{Cr}}{{\text{O}}_{\text{5}}}.$

Let x be the oxidation number of Cr.

$x + 1\left( { - 2} \right) + 4\left( { - 1} \right) = 0 \\\ x = + 6 \\\$
The oxidation number of Chromium in $Cr{O_5}$ is ${\text{ + 6}}{\text{.}}$

Hence, Option B is the correct answer.

Note:
We must know that the four of the oxygen atoms present in $Cr{O_5}$ exists as peroxides, and therefore their oxidation number is ${\text{ - 1}}{\text{.}}$