Question
Question: $\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}, \overrightarrow{b} \times \overr...
a×b=c,b×c=d, where c=0, then
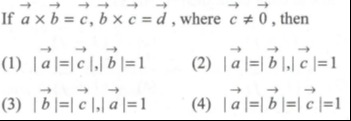
∣a∣=∣c∣,∣b∣=1
∣a∣=∣b∣,∣c∣=1
∣b∣=∣c∣,∣a∣=1
∣a∣=∣b∣=∣c∣=1
(1)
Solution
Given the vector equations:
- a×b=c
- b×c=d
Also, c=0.
From equation (1), c is perpendicular to b. Therefore, the angle between b and c is 90∘. From equation (2), the magnitude of d is given by: ∣d∣=∣b∣∣c∣sin(90∘)=∣b∣∣c∣ (Equation A)
Substitute c=a×b into the second equation: d=b×(a×b) Using the vector triple product identity A×(B×C)=(A⋅C)B−(A⋅B)C: d=(b⋅b)a−(b⋅a)b d=∣b∣2a−(a⋅b)b
For the options to be uniquely determined, we need an additional constraint. A common implicit constraint in such problems is that d is parallel to a. If d is parallel to a, then the component of d along b must be zero. This means (a⋅b)b=0. Since b=0 (otherwise c=0), it implies a⋅b=0. This means a is perpendicular to b (i.e., the angle between them, θab, is 90∘).
Under the condition a⊥b:
- The magnitude of c becomes: ∣c∣=∣a∣∣b∣sinθab=∣a∣∣b∣sin(90∘)=∣a∣∣b∣ (Equation B)
- The expression for d simplifies to: d=∣b∣2a−(0)b=∣b∣2a Taking the magnitude, ∣d∣=∣b∣2∣a∣ (Equation C)
Now, equate Equation A and Equation C: ∣b∣∣c∣=∣b∣2∣a∣ Since ∣b∣=0, we can divide by ∣b∣: ∣c∣=∣b∣∣a∣ This relation is identical to Equation B, confirming consistency.
Now, let's check which option satisfies these conditions. Consider option (1): ∣a∣=∣c∣ and ∣b∣=1. Substitute these into the derived relation ∣c∣=∣a∣∣b∣: ∣a∣=∣a∣(1) ∣a∣=∣a∣ This is consistent. Therefore, option (1) is a possible solution under the implicit assumption that d is parallel to a.
