Question
Question: $\overrightarrow{a}$, $\overrightarrow{b}$ and $\overrightarrow{c}$ are coplanar vectors such that $...
a, b and c are coplanar vectors such that ∣a∣=2, ∣b∣=3 & a∧b=30∘. A unit vector d is perpendicular to all of them. If (a×b)×(c×d)=6i^−3j^+3k^, then ∣c.i^∣+∣c.j^∣+∣c.k^∣ is equal to ____
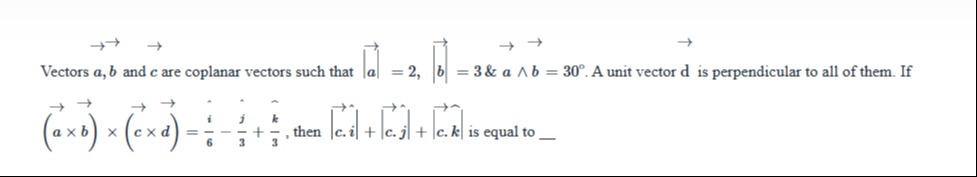
185
187
1811
1813
185
Solution
The coplanarity of a,b,c implies (a×b)⋅c=0. The magnitude of the cross product ∣a×b∣=∣a∣∣b∣sin(30∘)=2×3×21=3. Since d is a unit vector perpendicular to a and b, a×b is parallel to d, so a×b=±3d.
Using the vector triple product identity X×(Y×Z)=(X⋅Z)Y−(X⋅Y)Z, we simplify the given equation: (a×b)×(c×d)=(±3d)×(c×d) =±3[d×(c×d)] =±3[(d⋅d)c−(d⋅c)d] Since d is a unit vector, d⋅d=1. Since d is perpendicular to c, d⋅c=0. So, the expression becomes ±3[1⋅c−0⋅d]=±3c.
Equating this to the given vector: ±3c=6i^−3j^+3k^ c=±31(6i^−3j^+3k^)
Let c=cxi^+cyj^+czk^. We need to find ∣cx∣+∣cy∣+∣cz∣. In either case (±): c=31(6i^−3j^+3k^) or c=−31(6i^−3j^+3k^). The components of c will be ±181, ∓91, ±91. The absolute values of the components are 181, 91, 91.
Therefore, ∣c.i^∣+∣c.j^∣+∣c.k^∣=±181+∓91+±91=181+91+91=181+182+182=185.
