Solveeit Logo
Login

Question

Question: \[\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}\] can also be written as \[a)\overright...

A→+B→+C→\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C} can also be written as
a)C→+B→+A→a)\overrightarrow{C}+\overrightarrow{B}+\overrightarrow{A}
b)B→−C→−A→b)\overrightarrow{B}-\overrightarrow{C}-\overrightarrow{A}
c)A→+B→−C→c)\overrightarrow{A}+\overrightarrow{B}-\overrightarrow{C}
d)−A→−B→−C→d)-\overrightarrow{A}-\overrightarrow{B}-\overrightarrow{C}

Explanation

Solution

Here it follows the properties of vector addition and we can easily justify the correct statement simply by justifying the properties theoretically or diagrammatically. The diagram method for justifying the properties follows either the triangle law of vector addition or parallelogram law of vector addition.

Complete answer:
Here vector sum of this expression
A→+B→+C→\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C} can be theoretically written as vector sum as
C→+B→+A→\overrightarrow{C}+\overrightarrow{B}+\overrightarrow{A}which means both are written in equivalent manner only the vector diagram representation is different. Since the sum of two vectors can be done by Triangle Law of vector addition or parallelogram of vector addition.
When the head and tail of two vectors are joined together then the resultant is obtained by the third side of the triangle taken in opposite order which is represented by triangle law of vector addition.
The figure shows the triangle law of vector addition.

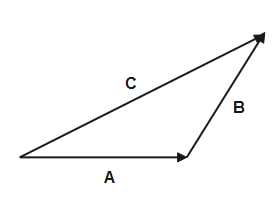
When both the vectors are joined to same point like tail & tail or head & head then the resultant is obtained by diagonal of that parallelogram drawn from common point of parallelogram. This figure shows the parallelogram law of vector addition.

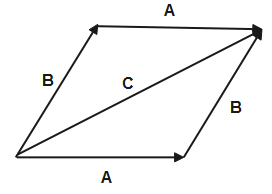
The Result obtained from both the laws is the same ; only the implementation method is different.
Properties of Vector Addition
1. Vector addition always follows commutative law, which states the order of addition doesn't matter:
A→+B→=B→+A→\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{B}+\overrightarrow{A}
Similarly in the given question it is also following the commutative law of vector addition so the sum of three vectors is always the sum of three vectors taken in different order.
2. Vector addition always follows associative law, which states that the sum of three vectors does not depend on which pair of vectors is added first: -
(A→+B→)+C→=A→+(B→+C→)(\overrightarrow{A}+\overrightarrow{B})+\overrightarrow{C}=\overrightarrow{A}+(\overrightarrow{B}+\overrightarrow{C})
Vector addition of more than two vectors can be done by the polygon law of vector addition, this law is the extended version of triangle law of vector addition.

So, Correct Option is A.

Note:
Vector always follows addition, subtraction and multiplication laws. Whenever we have to use a vector addition method then we have to observe the two vectors are joined in which manner because according to that we will choose triangle law of vector addition or parallelogram law of vector addition.