Solveeit Logo
Login

Question

Question: \[\overleftrightarrow {PQ}\]is perpendicular to \[\overleftrightarrow {RS}\]is symbolically written ...

PQ↔\overleftrightarrow {PQ}is perpendicular to RS↔\overleftrightarrow {RS}is symbolically written as:
A. PQ↔⊥RS↔\overleftrightarrow {PQ} \bot \overleftrightarrow {RS}
B. PQ↔∥RS↔\overleftrightarrow {PQ}\parallel \overleftrightarrow {RS}
C. PQ↔≠RS↔\overleftrightarrow {PQ} \ne \overleftrightarrow {RS}
D. PQ↔=RS↔\overleftrightarrow {PQ} = \overleftrightarrow {RS}

Explanation

Solution

A line is said to be perpendicular to another line if the angle between them is 90 degree. The property of perpendicularity is the relationship between two lines which makes a right angle. The two nonvertical lines are said to be perpendicular if they lie on the same plane and meet at the right angle. Two lines which are perpendicular to each other are horizontal and vertical lines. The slopes of two perpendicular lines are in negative reciprocals.
In this question, four options are given, and each has different symbols; hence we will approach the question by checking each option one by one and find which options have the correct option for perpendicular lines.

Complete step by step solution:
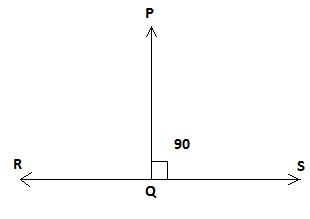
A. PQ↔⊥RS↔\overleftrightarrow {PQ} \bot \overleftrightarrow {RS}
Here symbol ⊥\botrepresents that the two lines line PQ and line RS make an angle of 90 degrees, i.e. they meet at a right angle as shown in the diagram below; hence they are perpendicular. Here line PQ is the vertical line, and the line RS is a horizontal line.

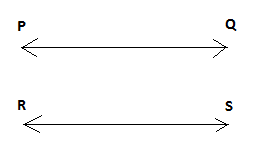
B. PQ↔∥RS↔\overleftrightarrow {PQ}\parallel \overleftrightarrow {RS}
Here symbol ∥\parallel represents that the two lines line PQ and line RS are parallel to each other since they are at the same distance apart everywhere as shown in the diagram. We can see the slope of both the lines are the same and their y-intercept is the same.

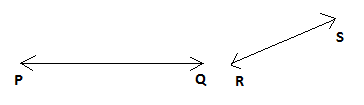
C. PQ↔≠RS↔\overleftrightarrow {PQ} \ne \overleftrightarrow {RS}
Here the symbol≠\ne represents that the two lines line PQ and lines RS are not equal, i.e. neither their slope nor their length is equal.

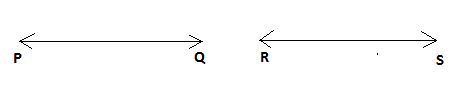
D. PQ↔=RS↔\overleftrightarrow {PQ} = \overleftrightarrow {RS}
Here the symbol = represents that the two lines line PQ and lines RS are equal as their slope and their length is equal.

Since the perpendicular lines are represented by the symbol ⊥\bot,
hence we can say option A is correct.

Note:
It is interesting to note here that the product of the slopes of the two perpendicular lines are always equals to -1. In other words, we can say that the slopes of the perpendicular lines are negative reciprocal of each other.