Question

A projectile is fired from the base of cone-shaped hill. The projectile grazes the vertex and strikes the hill again at the base. If $\alpha$ be the half-angle of the cone, h its height, u the initial velocity of projection and $\theta$ is angle of projection, then $tan\theta tan\alpha$ is

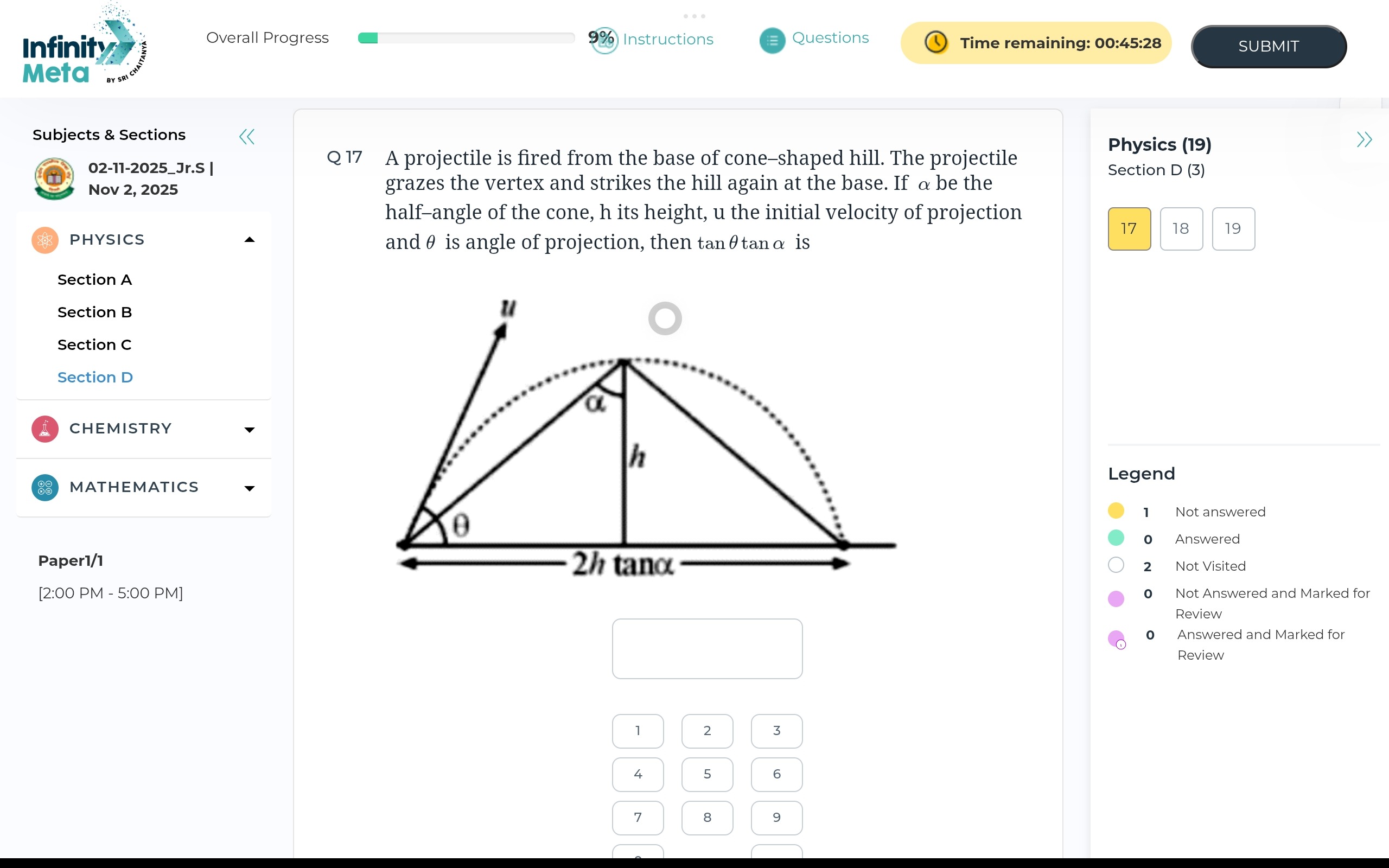
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (B)

2

Answer 2

The range of the projectile is $R = 2h \tan\alpha$. The vertex of the trajectory is at height $h$. The height of the vertex of a projectile is given by $y_v = \frac{u^2 \sin^2\theta}{2g}$. Thus, $h = \frac{u^2 \sin^2\theta}{2g}$. The range of the projectile is also given by $R = \frac{u^2 \sin(2\theta)}{g}$. Substituting $R = 2h \tan\alpha$, we get $2h \tan\alpha = \frac{u^2 \sin(2\theta)}{g}$. Substituting $h = \frac{u^2 \sin^2\theta}{2g}$ into the range equation gives $\frac{u^2 \sin^2\theta}{g} \tan\alpha = \frac{u^2 \sin(2\theta)}{g}$. Simplifying, we get $\sin^2\theta \tan\alpha = \sin(2\theta) = 2\sin\theta\cos\theta$. Thus, $\sin\theta \tan\alpha = 2\cos\theta$, which leads to $\tan\theta \tan\alpha = 2$.