Question
Question: In a triangle ABC, let $\sqrt{\sin A} + \sqrt{\sin B} + \sqrt{\sin C} = \sqrt{12 \cos \frac{A}{2} \c...
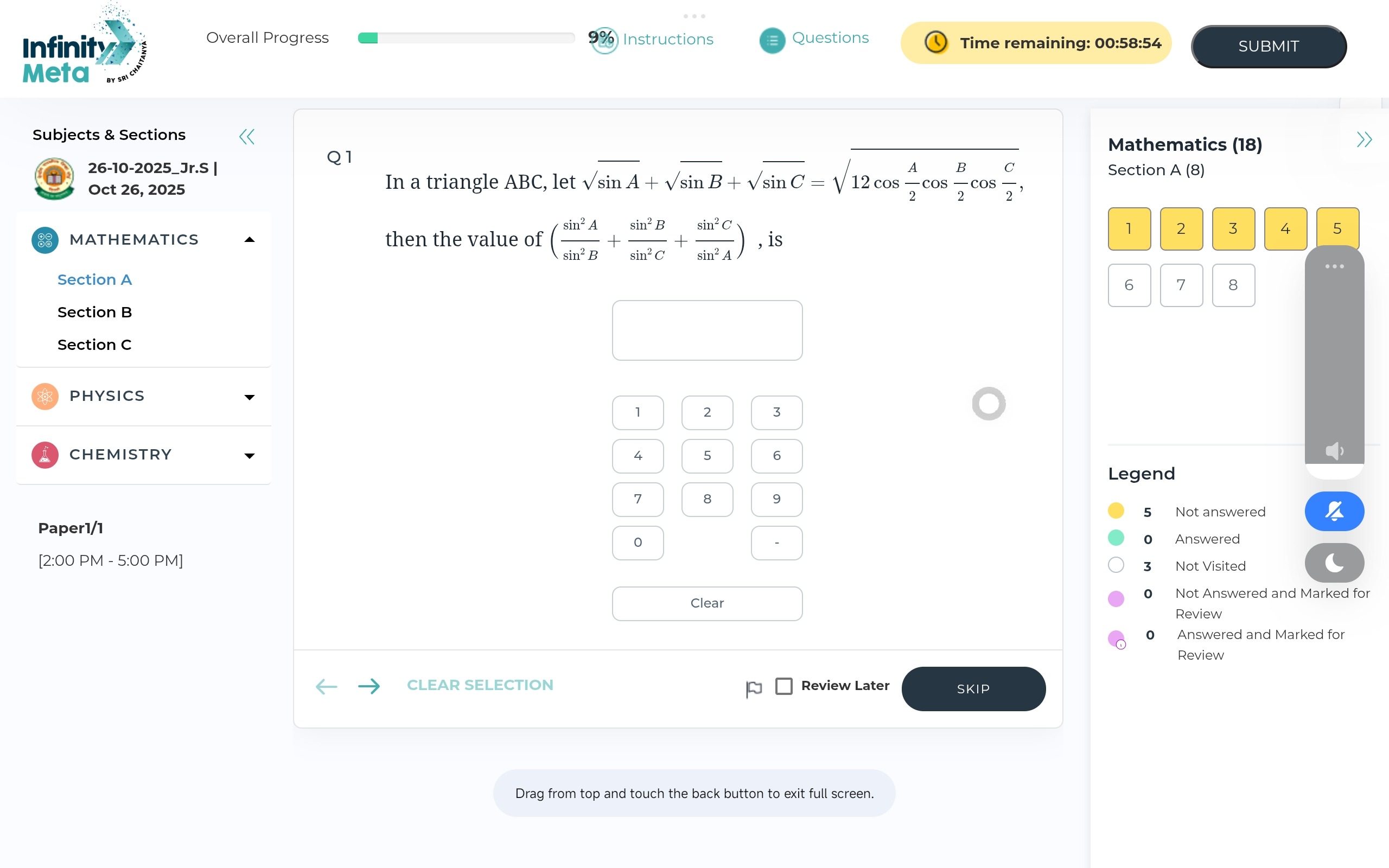
In a triangle ABC, let sinA+sinB+sinC=12cos2Acos2Bcos2C, then the value of (sin2Bsin2A+sin2Csin2B+sin2Asin2C), is
A
1
B
2
C
3
D
4
Answer
3
Explanation
Solution
The given condition is sinA+sinB+sinC=12cos2Acos2Bcos2C. For an equilateral triangle (A=B=C=60∘), LHS = 3sin60∘=323 and RHS = 12cos330∘=12(23)3=12833=293. Squaring both sides, 9⋅23=293, which matches.
Squaring the given equation and using identities, we can show that the condition implies A=B=C=60∘. Since A=B=C, sinA=sinB=sinC. Therefore, sin2Bsin2A=1, sin2Csin2B=1, and sin2Asin2C=1. The value of the expression is 1+1+1=3.
