Question

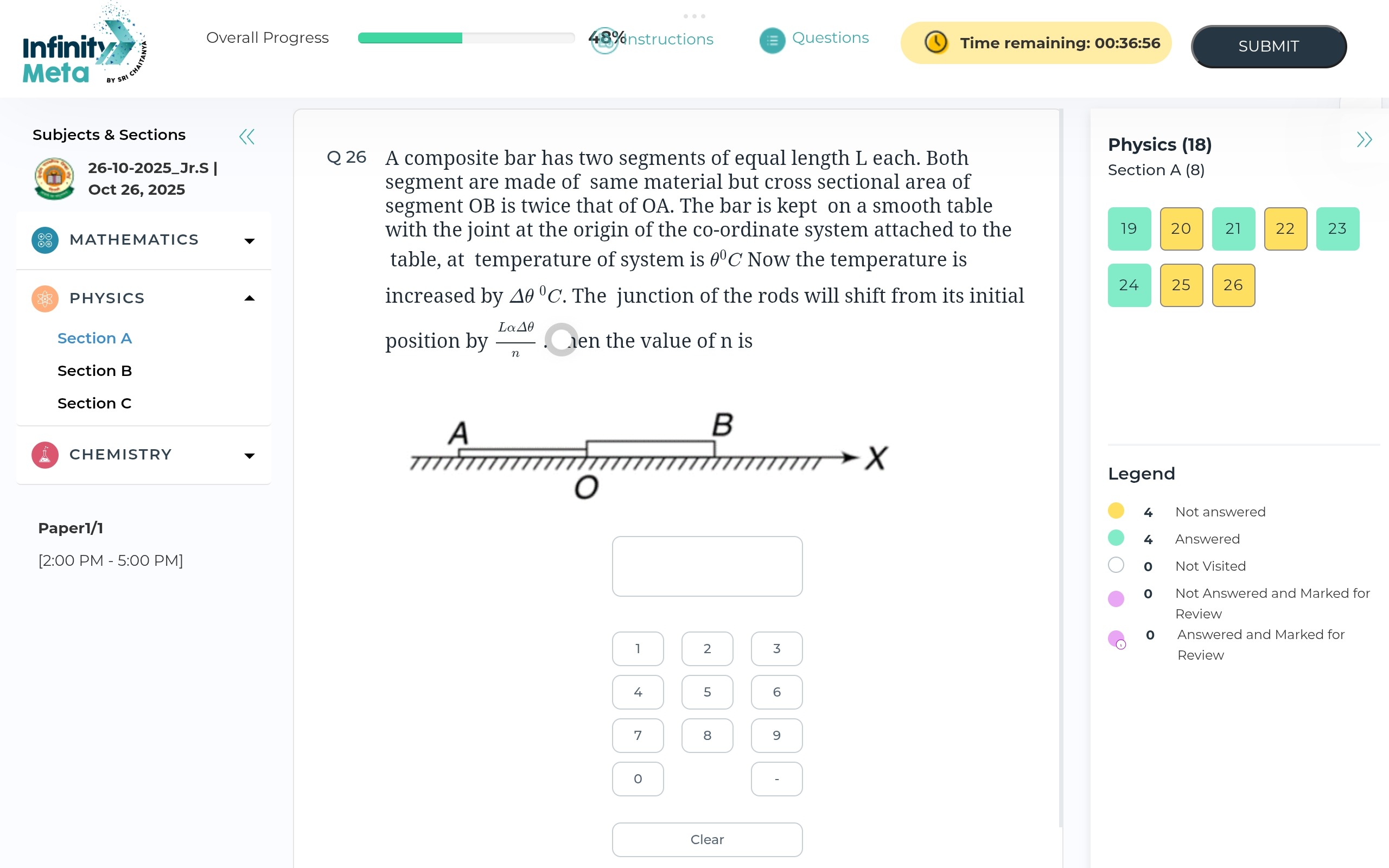
A composite bar has two segments of equal length L each. Both segment are made of same material but cross sectional area of segment OB is twice that of OA. The bar is kept on a smooth table with the joint at the origin of the co-ordinate system attached to the table, at temperature of system is $\theta$°C Now the temperature is increased by $\Delta\theta$ °C. The junction of the rods will shift from its initial position by $\frac{L\alpha\Delta\theta}{n}$. Then the value of n is

• A. 1
• B. 2
• C. 3
• D. -3

Answer 1

Answer: (D)

-3

Answer 2

Let the cross-sectional area of segment OA be $A$ and that of segment OB be $2A$. Both segments have length $L$ and are made of the same material with coefficient of linear thermal expansion $\alpha$. The temperature is increased by $\Delta\theta$.

The strain in segment OA is $\epsilon_{OA} = \alpha\Delta\theta + \frac{\sigma_{OA}}{E}$. The strain in segment OB is $\epsilon_{OB} = \alpha\Delta\theta + \frac{\sigma_{OB}}{E}$.

Since the bar is on a smooth table, there are no external horizontal forces. The forces at the joint must be in equilibrium. Assuming OA is to the left of the joint and OB is to the right, and $\sigma$ represents tensile stress, the force exerted by OA on the joint is $-\sigma_{OA}A$ and by OB is $\sigma_{OB}(2A)$. For equilibrium, $-\sigma_{OA}A + \sigma_{OB}(2A) = 0$, which gives $\sigma_{OA} = 2\sigma_{OB}$.

Let the initial position of OA be from $-L$ to $0$ and OB be from $0$ to $L$. The joint is initially at $0$. Let the final position of the joint be $x_j$. The displacement of the joint is related to the strain in each segment: $x_j = L\epsilon_{OA}$ $-x_j = L\epsilon_{OB}$

Substituting these into the strain equations: $\frac{x_j}{L} = \alpha\Delta\theta + \frac{\sigma_{OA}}{E}$ $-\frac{x_j}{L} = \alpha\Delta\theta + \frac{\sigma_{OB}}{E}$

Using $\sigma_{OA} = 2\sigma_{OB}$: $\frac{x_j}{L} = \alpha\Delta\theta + \frac{2\sigma_{OB}}{E}$ (1) $-\frac{x_j}{L} = \alpha\Delta\theta + \frac{\sigma_{OB}}{E}$ (2)

From (2), $\frac{\sigma_{OB}}{E} = -\frac{x_j}{L} - \alpha\Delta\theta$. Substitute this into (1): $\frac{x_j}{L} = \alpha\Delta\theta + 2\left(-\frac{x_j}{L} - \alpha\Delta\theta\right)$ $\frac{x_j}{L} = \alpha\Delta\theta - \frac{2x_j}{L} - 2\alpha\Delta\theta$ $\frac{3x_j}{L} = -\alpha\Delta\theta$ $x_j = -\frac{L\alpha\Delta\theta}{3}$

The junction shifts from its initial position by $x_j$. The problem states this shift is $\frac{L\alpha\Delta\theta}{n}$. Comparing the two expressions for the shift: $\frac{L\alpha\Delta\theta}{n} = -\frac{L\alpha\Delta\theta}{3}$ $n = -3$