Question
Question: If $x, y \in R, X = [x \quad y \quad 1]^T, A = \begin{bmatrix} 5 & 3 & -1 \\ 3 & 2 & -1 \\ -1 & -1 &...
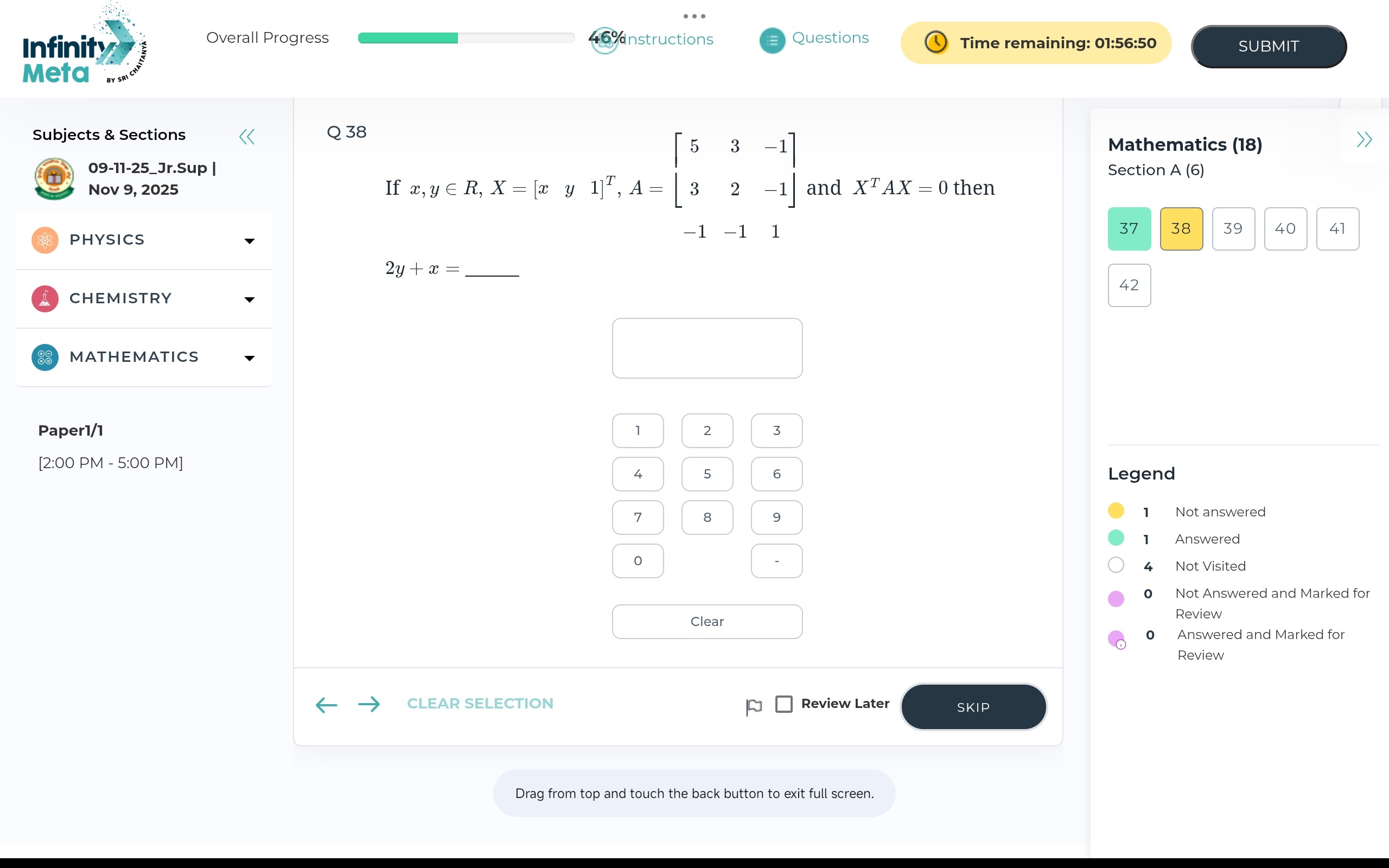
If x,y∈R,X=[xy1]T,A=53−132−1−1−11 and XTAX=0 then 2y+x=___
3
Solution
The given equation is XTAX=0. XTAX=[xy1]53−132−1−1−11xy1 XTAX=[xy1]5x+3y−13x+2y−1−x−y+1 XTAX=x(5x+3y−1)+y(3x+2y−1)+1(−x−y+1) XTAX=5x2+3xy−x+3xy+2y2−y−x−y+1 XTAX=5x2+6xy+2y2−2x−2y+1 Given XTAX=0, so 5x2+6xy+2y2−2x−2y+1=0. Let k=2y+x. Then x=k−2y. Substituting x in the equation: 5(k−2y)2+6(k−2y)y+2y2−2(k−2y)−2y+1=0 5(k2−4ky+4y2)+6ky−12y2+2y2−2k+4y−2y+1=0 5k2−20ky+20y2+6ky−12y2+2y2−2k+2y+1=0 (20−12+2)y2+(−20k+6k+2)y+(5k2−2k+1)=0 10y2+(−14k+2)y+(5k2−2k+1)=0 For real solutions of y, the discriminant must be non-negative. Δ=(−14k+2)2−4(10)(5k2−2k+1)≥0 4(1−7k)2−40(5k2−2k+1)≥0 4(1−14k+49k2)−200k2+80k−40≥0 4−56k+196k2−200k2+80k−40≥0 −4k2+24k−36≥0 k2−6k+9≤0 (k−3)2≤0 Since (k−3)2 cannot be negative, (k−3)2=0, which implies k=3. Therefore, 2y+x=3.
