Question

Two rods 1 and 2 of length 2l and l, thermal conductivities 2 k and 3 k are joined end to end. The area of cross-sectional of each rod be A. This composite rod is connected with another rod 3 of length 3l and conductivity k’. The area of cross-section of the rod 3 is 2A. If the rod 3 conducts the heat two times that through the other rods, find the value of $\frac{4k'}{k}$.

Answer 1

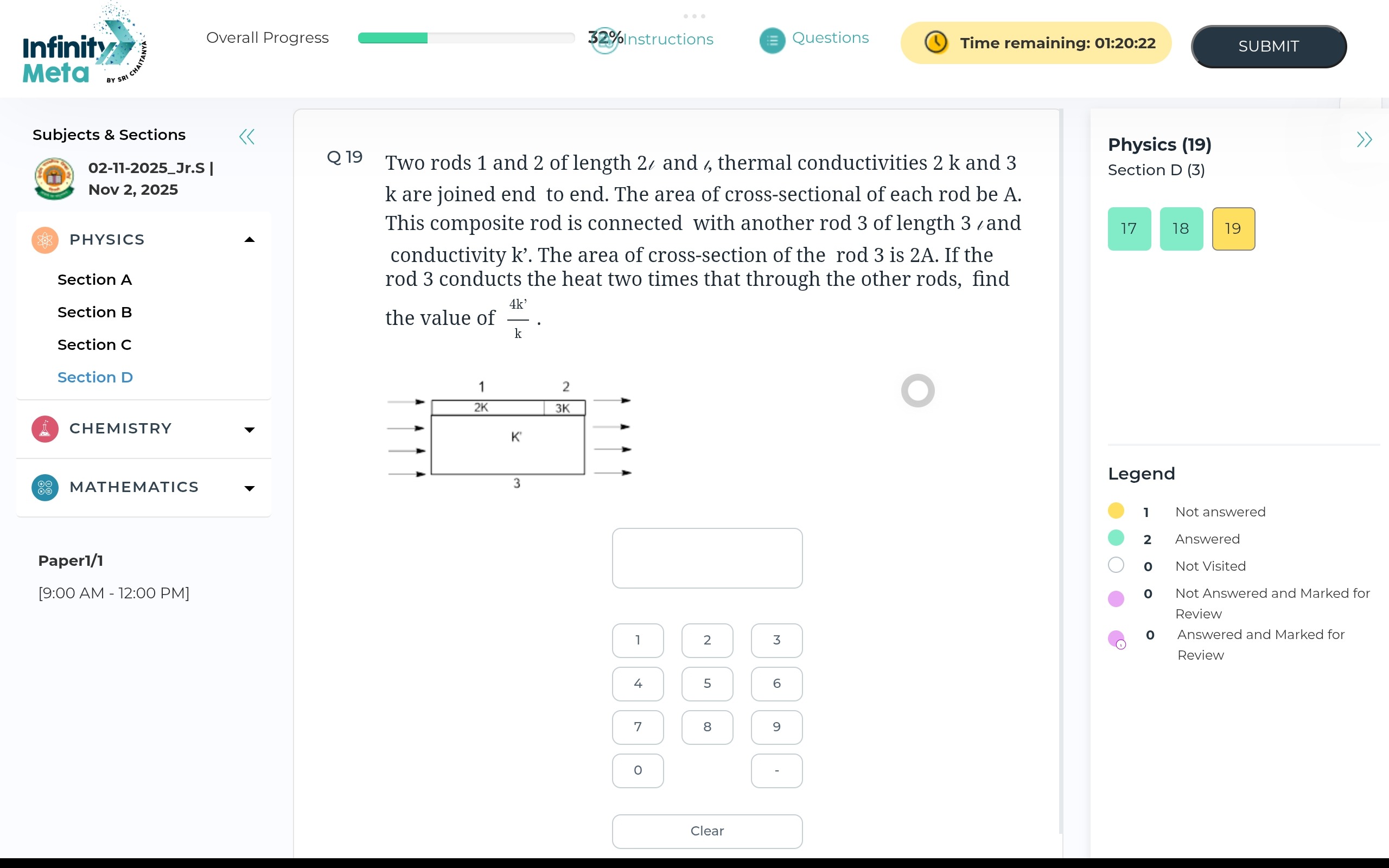
9

Answer 2

Rods 1 and 2 are in series, their combined resistance is $R_{12} = R_1 + R_2 = \frac{2l}{(2k)A} + \frac{l}{(3k)A} = \frac{l}{kA} + \frac{l}{3kA} = \frac{4l}{3kA}$. The condition that rod 3 conducts heat two times that through the other rods implies a parallel connection where $\Delta T$ is the same across all rods. Thus, $Q_3 = 2Q_{12}$. Since $Q = \frac{\Delta T}{R}$, we have $\frac{\Delta T}{R_3} = 2 \frac{\Delta T}{R_{12}}$, which simplifies to $R_{12} = 2R_3$. The resistance of rod 3 is $R_3 = \frac{3l}{k'(2A)} = \frac{3l}{2Ak'}$. Equating the resistances: $\frac{4l}{3kA} = 2 \left( \frac{3l}{2Ak'} \right) = \frac{3l}{Ak'}$. Canceling $l$ and $A$, we get $\frac{4}{3k} = \frac{3}{k'}$. This gives $4k' = 9k$, so $\frac{k'}{k} = \frac{9}{4}$. The required value is $\frac{4k'}{k} = 4 \times \frac{9}{4} = 9$.