Question

Out of 800 boys in a school 224 played cricket, 240 played hockey and 236 played basketball. Of the total 64 played both basketball and hockey, 80 played cricket and basketball and 40 played cricket and hockey, 24 players all the three games. The number of boys who did not play any game is
A. 128
B. 216
C. 240
D. 260

Answer 1

Hint: Let us draw a Venn’s diagram of boys in different games of the school, and find the number of boys that play any of the games (each boy should be counted only once).

Complete step-by-step answer:

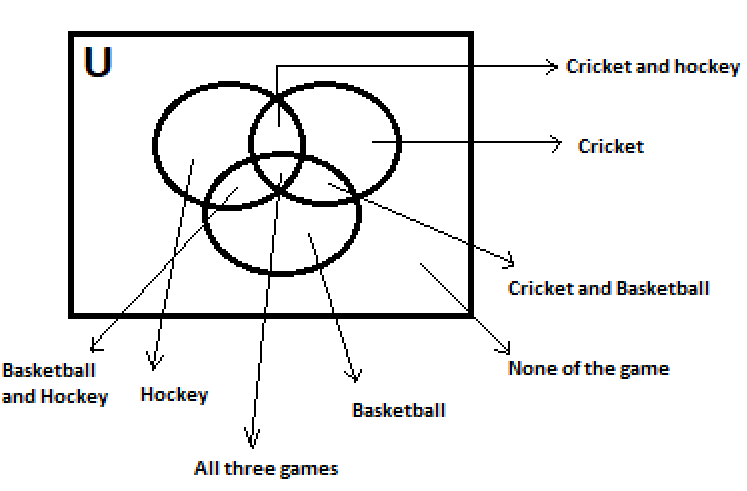
Now to find the number of boys who did not play any game, we first find the total number of boys that play any game, but each boy should be counted only once. And then subtract that by the total number of boys.
Now as we can see from the above diagram that the number of boys that only play cricket will be equal to the total number of boys that play cricket – number of boys that play cricket and basketball both – number of boys that play cricket and hockey both + number of boys that play all the three games.
We add the number of boys that play all three games because it is subtracted twice when we subtracted the number of boys who play cricket and hockey and the number of boys who play cricket and basketball.
So, the total number of boys who only play only cricket will be 224 – 80 – 40 + 24 = 128.
And the number of boys who play basketball is 236.
And the number of boys who play hockey is 240.
So, now as we can see from the above Venn’s diagram that total number of boys who pays any of the game (each boy is counted only once) will be equal to number of boys who plays only cricket + number of boys who plays basketball + number of boys who plays hockey – number of boys who plays hockey and basketball both.
Now we have subtracted the number of boys who play basketball and hockey both because it is counted twice when we add the number of boys who play basketball and the number of boys who play hockey.
And, the number of boys who play basketball and hockey both is 64.
So, the total number of boys who play any of the games (each boy is counted only once) = 128 + 236 + 240 – 64 = 540.
Now we know the number of boys who play any of the games (each boy is counted only once) = 540.
And the total number of boys in the school is 800.
So, the number of boys who do not play any game will be the total number of boys – number of boys who play any of the games = 800 – 540 = 260.
Hence, the correct option will be D.

Note: Whenever we come up with this type of problem then we had to first, draw Venn’ diagram and then we have to find number of boys that play any of the game we add number of boys that only play cricket and then add that with number of boys that play hockey and number of boys that play basketball and then subtract number of boys that play hockey and basketball both (because it is counted twice). After that we subtract that with the total number of boys to get the required answer.