Orthocentre of the triangle whose vertices are (0, 0) (2, –1... | MATH - POINTS RELATE TO TRIANGLE (ORTHOCENTRE,...) | SolveeIt

Orthocentre of the triangle whose vertices are (0, 0) (2, –1) and (1, 3) is.

$\left( \frac{4}{7},\frac{1}{7} \right)$

$\left( - \frac{4}{7}, - \frac{1}{7} \right)$

(–4, –1)

(4, 1)

Answer

$\left( - \frac{4}{7}, - \frac{1}{7} \right)$

Explanation

Equation of line BC is $4 x + y = 7$ , then equation of line AD is $x - 4 y + k = 0$ but it passes through (0,0) hence $k = 0$

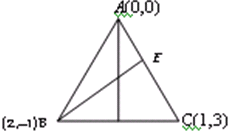
thus equation of $A D = x - 4 y = 0$ .....(i)

Similarly the equation of $A C = 3 x - y = 0$ and BE is

$x + 3 y + 1 = 0$ .....(ii)

On solving (i) and (ii), the required orthocentre is $\left( \frac { - 4 } { 7 } , \frac { - 1 } { 7 } \right)$ .

Question: Orthocentre of the triangle whose vertices are (0, 0) (2, –1) and (1, 3) is....