Question

Optical axis of a thin equi-convex lens is the X-axis. The coordinate of a point object and its images are $( - 20cm\,,1\,cm)$ and $(25\,cm\,, - 2\,cm)$ respectively
A. The lens is located at $x = 5\,cm$
B. The lens is located at $x = \, - 5\,cm$
C. The focal length of the lens is $10\,cm$
D. The focal length of the lens is $15\,cm$

Answer 1

A lens can be classified by the curvature of two optical surfaces. A lens is said to be a biconvex lens or double convex lens if both the surfaces of the lens are convex. An equi-convex lens is the lens in which surfaces of the lenses have the same radius of curvature.

Complete step by step answer:
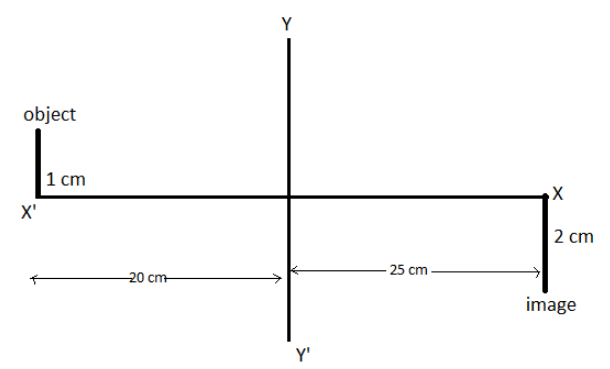
Now, it is given in the question, object and image is placed in x-y plane such that the coordinates of a point object and images are $( - 20cm\,,1\,cm)$ and $(25\,cm\,, - 2\,cm)$.
Therefore, we can say that, the distance of the object from the origin $= \,25\,cm$
Also, the distance of the image from the origin $= \, - 20\,cm$
The size of the object $= \,1\,cm$
And, size of the image $= \, - 2\,cm$

Therefore, the magnification is given by
$m = \dfrac{v}{u}$
Where, $v$ is the size of the image and $u$ is the size of the object.
Therefore, by putting the values of $v$ and $u$ , we get
$m = \dfrac{{ - 2}}{1}$
$\Rightarrow \,m = - 2$
Now, negative sign here means that the image is real and inverted.
Now, for finding the position of lens, taking magnitude of $v$ and $u$ , we get
$\left| {\dfrac{v}{u}} \right| = 2$
$\left| v \right| = 2\left| u \right|$
Now, adding $\left| v \right|$ and $\left| u \right|$ , we get
$\left| u \right| + \left| v \right| =$ distance of object from the lens + distance of lens from the lens
$\therefore \,u + 2u = 25 - ( - 20)$
$\Rightarrow \,3u = 25 + 20$
$\Rightarrow \,3u = 45$
$\Rightarrow \,u = 15$
Therefore, the distance of the object from the lens is $u = 15\,cm$
Now, distance of the image from the lens is $\left| v \right| = 2\left| u \right| = 30\,cm$

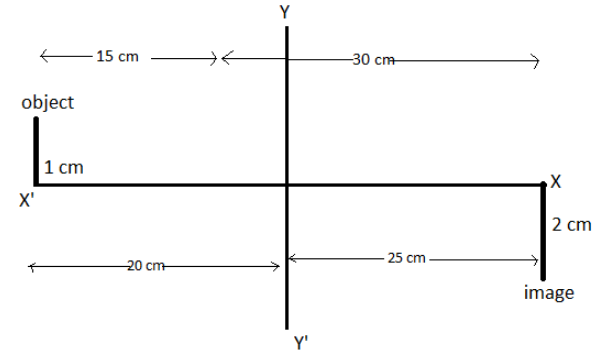
Therefore, the lens is placed at $x = - 5\,cm$

Hence, option B is the correct option.

Note: Here, magnification is used to determine the nature of the image. Therefore, we got a real and inverted image. Real images are made by the converging rays where all the focus points are collected. An example of a real image is a cinema screen.