Question

$OPQ$ is a sector of a circle with center $O$ and radius 15 cm. If $m\angle POQ = 30^\circ$, find the area enclosed by the arc $PQ$ and the chord $PQ$.

Answer 1

Here, we need to find the area of the minor segment enclosed by the arc and the chord. To solve this question, we will find the area of the sector $OPQ$ and the area of the triangle $OPQ$. Then, we will subtract these to get the required area of the minor segment.

Formula Used: The area of a sector of a circle is given by the formula $\dfrac{\theta }{{360^\circ }}\pi {r^2}$, where $r$ is the radius of the circle and $\theta$ is the angle between the two radii forming the sector.
The area of a triangle can be calculated using the length of any two of its sides $a$ and $b$, and the angle between them $C$ using the formula $\dfrac{1}{2}ab\sin C$.

Complete step-by-step answer:
We will find the areas of sector $OPQ$ and triangle $OPQ$, and subtract them to get the required area enclosed by the arc $PQ$ and the chord $PQ$.
First, we will draw the diagram using the given information.

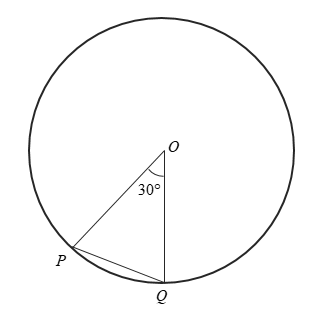
Here, $OP$ and $OQ$ are radii of the circle of 15 cm length.
We have to find the area enclosed by the arc $PQ$ and the chord $PQ$, that is the area of the minor segment .
First, we will find the area of the sector $OPQ$.
We know that the area of a sector of a circle is given by the formula $\dfrac{\theta }{{360^\circ }}\pi {r^2}$, where $r$ is the radius of the circle and $\theta$ is the angle between the two radii forming the sector.
Substituting $\theta = 30^\circ$ and $r = 15{\rm{ cm}}$, we get
Area of sector $OPQ$ $= \dfrac{{30^\circ }}{{360^\circ }}\pi {\left( {15} \right)^2}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow \dfrac{{30^\circ }}{{360^\circ }}\pi {\left( {15} \right)^2} = \dfrac{1}{{12}}\pi \left( {225} \right)\\\ \Rightarrow \dfrac{{30^\circ }}{{360^\circ }}\pi {\left( {15} \right)^2} = \dfrac{{75}}{4}\pi \end{array}$
Substituting $\pi$ as $\dfrac{{22}}{7}$, we get
$\begin{array}{l} \Rightarrow \dfrac{{30^\circ }}{{360^\circ }}\pi {\left( {15} \right)^2} = \dfrac{{75}}{{14}} \times \dfrac{{22}}{7}\\\ \Rightarrow \dfrac{{30^\circ }}{{360^\circ }}\pi {\left( {15} \right)^2} = \dfrac{{825}}{{14}}\end{array}$
Therefore, the area of the sector $OPQ$ is $\dfrac{{825}}{{14}}{\rm{ c}}{{\rm{m}}^2}$.
Now, we will find the area of the triangle $OPQ$.
The area of a triangle can be calculated using the length of any two of its sides $a$ and $b$, and the angle between them $C$ using the formula $\dfrac{1}{2}ab\sin C$.
Therefore, we get the area of the triangle $OPQ$ as $\dfrac{1}{2}\left( {OP} \right)\left( {OQ} \right)\sin \angle POQ$.
Substituting $OP = 15{\rm{ cm}}$, $OQ = 15{\rm{ cm}}$, and $\angle POQ = 30^\circ$, we get
Area of triangle $OPQ$ $= \dfrac{1}{2}\left( {15} \right)\left( {15} \right)\sin 30^\circ$
Simplifying the expression, we get
$\Rightarrow \dfrac{1}{2}\left( {15} \right)\left( {15} \right)\sin 30^\circ = \dfrac{{225}}{2}\sin 30^\circ$
We know that the sine of the angle measuring $30^\circ$ is $\dfrac{1}{2}$.
Substituting $\sin 30^\circ = \dfrac{1}{2}$ in the expression, we get
$\begin{array}{l} \Rightarrow \dfrac{1}{2}\left( {15} \right)\left( {15} \right)\sin 30^\circ = \dfrac{{225}}{2} \times \dfrac{1}{2}\\\ \Rightarrow \dfrac{1}{2}\left( {15} \right)\left( {15} \right)\sin 30^\circ = \dfrac{{225}}{4}\end{array}$
Therefore, the area of the triangle $OPQ$ is $\dfrac{{225}}{4}{\rm{ c}}{{\rm{m}}^2}$.
Finally, we will subtract the area of the triangle$OPQ$ from the area of sector $OPQ$ to get the area enclosed by the arc $PQ$ and the chord $PQ$.
Therefore, we get
Area enclosed by arc $PQ$ and the chord $PQ$ $= \left( {\dfrac{{825}}{{14}} - \dfrac{{225}}{4}} \right){\rm{ c}}{{\rm{m}}^2}$
Taking the L.C.M., we get
$\Rightarrow \left( {\dfrac{{825}}{{14}} - \dfrac{{225}}{4}} \right){\rm{ c}}{{\rm{m}}^2} = \dfrac{{1650 - 1575}}{{28}}{\rm{ c}}{{\rm{m}}^2}$
Subtracting the terms in the numerator, we get
$\Rightarrow \left( {\dfrac{{825}}{{14}} - \dfrac{{225}}{4}} \right){\rm{ c}}{{\rm{m}}^2} = \dfrac{{75}}{{28}}{\rm{ c}}{{\rm{m}}^2}$
Dividing 75 by 28, we get
$\Rightarrow \left( {\dfrac{{825}}{{14}} - \dfrac{{225}}{4}} \right){\rm{ c}}{{\rm{m}}^2} = 2.68{\rm{ c}}{{\rm{m}}^2}$
$\therefore$ We get the area enclosed by arc $PQ$ and the chord $PQ$as $2.68{\rm{ c}}{{\rm{m}}^2}$.

Note: If we don’t remember the formula of a triangle $\dfrac{1}{2}ab\sin C$, we also find the area of the triangle $OPQ$ using the formula $\dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height}}$. Let as assume $AD$ be the height. Using trigonometric ratios, we can find the base and height of the isosceles triangle $OPQ$ as $\dfrac{{15\left( {\sqrt 3 - 1} \right)}}{{\sqrt 2 }}$ and $\dfrac{{15\left( {\sqrt 3 + 1} \right)}}{{2\sqrt 2 }}$ respectively.