Question

Opposite angles of a Rhombus are
$A$- Complementary
$B$- Equal
$C$- Supplementary
$D$- Never Equal

Answer 1

In order to solve such a type of question, the student must have an idea about the properties of geometric figures. The properties which student should be aware of for rhombus are as follows

All sides of the Rhombus are equal.
Opposite Sides of Rhombus are parallel.
Diagonals bisect each other at Right Angles.
Diagonals bisect the angles of the Rhombus.

Complete answer:

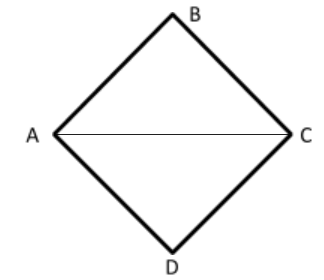
In the given figure ABCD is a Rhombus with Diagonal AC
We know from the properties of Rhombus that BC$||$AD, AC is a transversal, Since opposite sides of Rhombus are Parallel
So, $\angle ACB = \angle CAD......(1)$- Alternate Interior Angles are equal
Similarly we can say $\angle BAC = \angle ACD......(2)$
In $\vartriangle ABC\& \vartriangle ACD$, we have
$\angle ACB = \angle CAD$
$\angle BAC = \angle ACD$
Side AC is Common.
SO both the triangles are congruent by the Rule ASA
$\therefore \vartriangle ACB \cong \vartriangle ACD$
Thus We can say that $\angle ABC = \angle ADC.......(3)$
Adding Equation $1\& 2$ we get
$\begin{gathered} \angle ACB + \angle ACD = \angle CAD + \angle BAC \\\ OR,\angle BCD = \angle BAC...........(4) \\\ \end{gathered}$
So, from equation $3\& 4$, we can say that the opposite angles of rhombus are equal.
Hence Proved.

Answer to this question is Option $B$- Equal

Note: Though the property is asked directly in this question, it is always necessary to know how to prove it because most of the times the questions asked are about the proof. So the students should not rely on only learning the property but rather know how to prove the property.