Solveeit Logo
Login

Question

Question: $\operatorname{Tan}^{-1} \frac{c_{1}x - y}{c_{1}y + x} + \operatorname{Tan}^{-1} \frac{c_{2} - c_{1}...

Tan⁡−1c1x−yc1y+x+Tan⁡−1c2−c11+c2c1+Tan⁡−1c3−c21+c3c2+...Tan⁡−11cn=\operatorname{Tan}^{-1} \frac{c_{1}x - y}{c_{1}y + x} + \operatorname{Tan}^{-1} \frac{c_{2} - c_{1}}{1+c_{2}c_{1}} + \operatorname{Tan}^{-1} \frac{c_{3} - c_{2}}{1+c_{3}c_{2}} + ... \operatorname{Tan}^{-1} \frac{1}{c_{n}} =

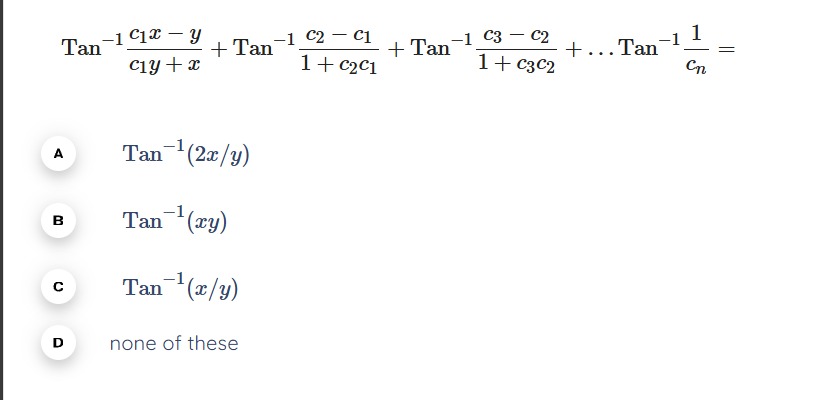
A

Tan⁡−1(2x/y)\operatorname{Tan}^{-1}(2x/y)

B

Tan⁡−1(xy)\operatorname{Tan}^{-1}(xy)

C

Tan⁡−1(x/y)\operatorname{Tan}^{-1}(x/y)

D

none of these

Answer

Tan⁡−1(x/y)\operatorname{Tan}^{-1}(x/y)

Explanation

Solution

The first term can be written as Tan⁡−1c1−y/x1+c1(y/x)=Tan⁡−1c1−Tan⁡−1(y/x)\operatorname{Tan}^{-1} \frac{c_{1} - y/x}{1 + c_{1}(y/x)} = \operatorname{Tan}^{-1} c_1 - \operatorname{Tan}^{-1} (y/x). The subsequent terms are of the form Tan⁡−1ck−ck−11+ckck−1=Tan⁡−1ck−Tan⁡−1ck−1\operatorname{Tan}^{-1} \frac{c_{k} - c_{k-1}}{1+c_{k}c_{k-1}} = \operatorname{Tan}^{-1} c_k - \operatorname{Tan}^{-1} c_{k-1}. The series becomes a telescoping sum: (Tan⁡−1c1−Tan⁡−1(y/x))+(Tan⁡−1c2−Tan⁡−1c1)+⋯+(Tan⁡−1cn−Tan⁡−1cn−1)+Tan⁡−11cn(\operatorname{Tan}^{-1} c_1 - \operatorname{Tan}^{-1} (y/x)) + (\operatorname{Tan}^{-1} c_2 - \operatorname{Tan}^{-1} c_1) + \dots + (\operatorname{Tan}^{-1} c_n - \operatorname{Tan}^{-1} c_{n-1}) + \operatorname{Tan}^{-1} \frac{1}{c_n} =Tan⁡−1cn−Tan⁡−1(y/x)+Tan⁡−11cn= \operatorname{Tan}^{-1} c_n - \operatorname{Tan}^{-1} (y/x) + \operatorname{Tan}^{-1} \frac{1}{c_n}. Assuming cn>0c_n > 0, we use Tan⁡−1θ+Tan⁡−1(1/θ)=π2\operatorname{Tan}^{-1} \theta + \operatorname{Tan}^{-1} (1/\theta) = \frac{\pi}{2}. So, Tan⁡−1cn+Tan⁡−11cn=π2\operatorname{Tan}^{-1} c_n + \operatorname{Tan}^{-1} \frac{1}{c_n} = \frac{\pi}{2}. The sum is π2−Tan⁡−1(y/x)\frac{\pi}{2} - \operatorname{Tan}^{-1} (y/x). Using π2=Tan⁡−1(x/y)+Tan⁡−1(y/x)\frac{\pi}{2} = \operatorname{Tan}^{-1} (x/y) + \operatorname{Tan}^{-1} (y/x) (for x/y>0x/y > 0), the sum is (Tan⁡−1(x/y)+Tan⁡−1(y/x))−Tan⁡−1(y/x)=Tan⁡−1(x/y)(\operatorname{Tan}^{-1} (x/y) + \operatorname{Tan}^{-1} (y/x)) - \operatorname{Tan}^{-1} (y/x) = \operatorname{Tan}^{-1} (x/y).