Question
Question: $\operatorname{Limit}_{x \rightarrow \pi / 2} \frac{\left(1-\tan \frac{x}{2}\right)(1-\sin x)}{\left...
Limitx→π/2(1+tan2x)(π−2x)3(1−tan2x)(1−sinx) is
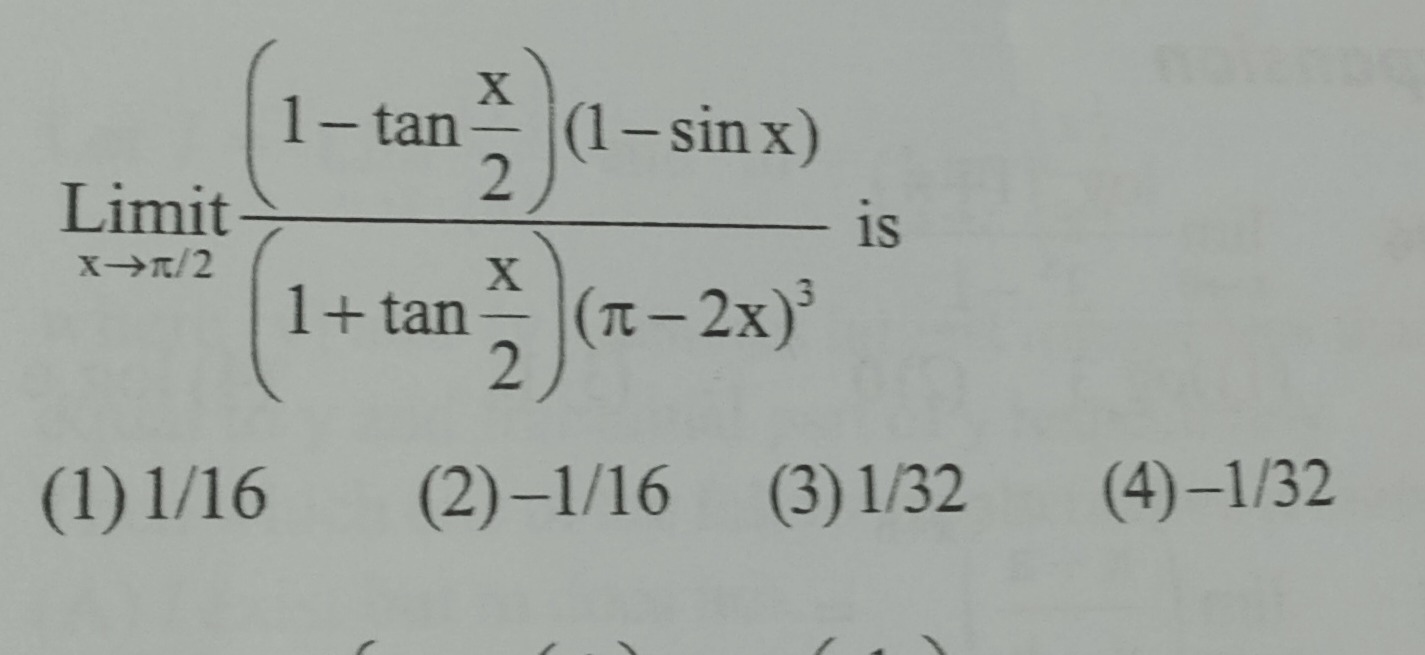
1/16
-1/16
1/32
-1/32
1/32
Solution
To evaluate the limit Limitx→π/2(1+tan2x)(π−2x)3(1−tan2x)(1−sinx), we observe that as x→π/2, the expression takes the indeterminate form 0/0.
We use the substitution method. Let x=2π−h.
As x→2π, h→0.
Now, substitute x=2π−h into the expression:
-
Numerator terms:
-
1−tan2x=1−tan(4π−2h)
Using the tangent subtraction formula tan(A−B)=1+tanAtanBtanA−tanB:
tan(4π−2h)=1+tan(π/4)tan(h/2)tan(π/4)−tan(h/2)=1+tan(h/2)1−tan(h/2)
So, 1−tan2x=1−1+tan(h/2)1−tan(h/2)=1+tan(h/2)(1+tan(h/2))−(1−tan(h/2))=1+tan(h/2)2tan(h/2). -
1−sinx=1−sin(2π−h)
Using the identity sin(π/2−θ)=cosθ:
1−sinx=1−cosh.
-
-
Denominator terms:
-
1+tan2x=1+tan(4π−2h)
1+tan2x=1+1+tan(h/2)1−tan(h/2)=1+tan(h/2)(1+tan(h/2))+(1−tan(h/2))=1+tan(h/2)2. -
π−2x=π−2(2π−h)=π−π+2h=2h.
Therefore, (π−2x)3=(2h)3=8h3.
-
Now substitute these back into the limit expression: Limith→0(1+tan(h/2)2)(8h3)(1+tan(h/2)2tan(h/2))(1−cosh) Cancel out the common term 1+tan(h/2)2 from the numerator and denominator: Limith→08h3tan(h/2)(1−cosh) We can rewrite this expression to use standard limits: Limith→0htan(h/2)⋅h21−cosh⋅81 We know the following standard limits:
- Limitθ→0θtanθ=1
- Limitθ→0θ21−cosθ=21
Apply these to our expression:
-
For htan(h/2): Multiply and divide by 2 to match the form θtanθ:
Limith→0htan(h/2)=Limith→0h/2tan(h/2)⋅21=1⋅21=21. -
For h21−cosh: This is a direct application of the standard limit:
Limith→0h21−cosh=21.
Now, substitute these limit values back into the expression: (21)⋅(21)⋅(81)=41⋅81=321
The value of the limit is 321.
