Solveeit Logo
Login

Question

Question: $\operatorname{Limit}_{x \rightarrow \infty}\left(\frac{x+2}{x-2}\right)^{x+1}=$...

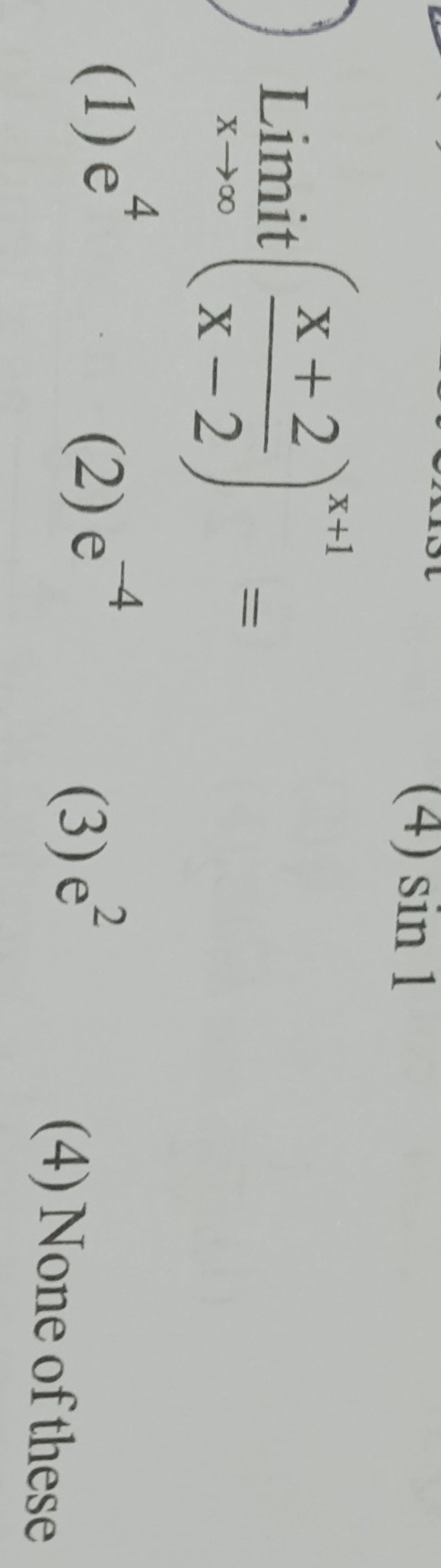
Limit⁡x→∞(x+2x−2)x+1=\operatorname{Limit}_{x \rightarrow \infty}\left(\frac{x+2}{x-2}\right)^{x+1}=

A

e4e^{4}

B

e−4e^{-4}

C

sin⁡1\sin 1

D

e2e^{2}

E

None of these

Answer

e4e^{4}

Explanation

Solution

The given limit is of the indeterminate form 1∞1^\infty. To evaluate, we use the formula:

Limit⁡x→a[f(x)]g(x)=eLimit⁡x→ag(x)[f(x)−1]\operatorname{Limit}_{x \rightarrow a} [f(x)]^{g(x)} = e^{\operatorname{Limit}_{x \rightarrow a} g(x)[f(x)-1]}

Here, f(x)=x+2x−2f(x) = \frac{x+2}{x-2} and g(x)=x+1g(x) = x+1.

  1. Calculate the exponent:

    Limit⁡x→∞(x+1)(x+2x−2−1)\operatorname{Limit}_{x \rightarrow \infty} (x+1)\left(\frac{x+2}{x-2}-1\right)

  2. Simplify the expression:

    (x+1)(x+2−(x−2)x−2)=(x+1)(4x−2)=4x+4x−2(x+1)\left(\frac{x+2-(x-2)}{x-2}\right) = (x+1)\left(\frac{4}{x-2}\right) = \frac{4x+4}{x-2}

  3. Evaluate the limit:

    Limit⁡x→∞4x+4x−2=Limit⁡x→∞4+4/x1−2/x=4+01−0=4\operatorname{Limit}_{x \rightarrow \infty} \frac{4x+4}{x-2} = \operatorname{Limit}_{x \rightarrow \infty} \frac{4+4/x}{1-2/x} = \frac{4+0}{1-0} = 4

Therefore, the original limit is e4e^4.