Question

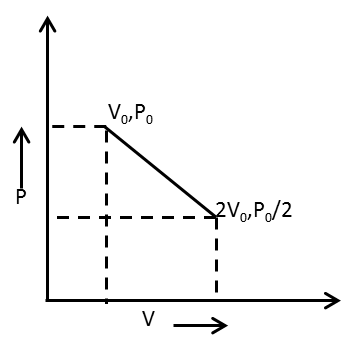
One ruble of gas expands obeying the relation as shown in the P-V diagram. The maximum temperature in this process is equal to

A. $\dfrac{{{P_0}{V_0}}}{R}$
B. $\dfrac{{3{P_0}{V_0}}}{R}$
C. $\dfrac{{9{P_0}{V_0}}}{{8R}}$
D. None of these

Answer 1

Determine the equation of for the given pressure-volume diagram. Use ideal gas equation for one mole of gas. Differentiate the equation for the temperature of gas with respect to volume and use the condition for the maximum temperature of the gas.

Formula used:
The ideal gas equation is given by
$PV = nRT$
Here, $P$ is the pressure, $V$ is volume, $n$ is the number of moles of gas, $R$ is the gas constant and $T$ is the temperature.

Complete step by step answer:
Rewrite equation (1) for the one mole of gas.
$PV = RT$
$\Rightarrow P = \dfrac{{RT}}{V}$

The P-V curve given has the equation in the form $y = mx + c$.

For the given P-V curve,
$y = P$, $x = V$, $c = \dfrac{{3{P_0}}}{2}$
$m = \dfrac{{{P_2} - {P_1}}}{{{V_2} - {V_1}}}$
$\Rightarrow m = \dfrac{{\dfrac{{{P_0}}}{2} - {P_0}}}{{2{V_0} - {V_0}}}$
$\Rightarrow m = - \dfrac{{{P_0}}}{{2{V_0}}}$

Hence, the equation of the given P-V curve is
$P = - \dfrac{{{P_0}}}{{2{V_0}}}V + \dfrac{{3{P_0}}}{2}$

Substitute $\dfrac{{RT}}{V}$ for $P$ in the above equation.
$\dfrac{{RT}}{V} = - \dfrac{{{P_0}}}{{2{V_0}}}V + \dfrac{{3{P_0}}}{2}$
$\Rightarrow T = - \dfrac{{{P_0}}}{{2{V_0}}}\dfrac{{{V^2}}}{R} + \dfrac{{3{P_0}}}{2}\dfrac{V}{R}$ …… (2)

Differentiate the above equation with respect to volume.
$\dfrac{{dT}}{{dV}} = - \dfrac{{{P_0}}}{{{V_0}}}\dfrac{V}{R} + \dfrac{{3{P_0}}}{{2R}}$

For the maximum temperature, the differentiation of temperature with respect to volume is zero.
$\dfrac{{dT}}{{dV}} = 0$

Substitute 0 for $\dfrac{{dT}}{{dV}}$ in the above equation.
$0 = - \dfrac{{{P_0}}}{{{V_0}}}\dfrac{V}{R} + \dfrac{{3{P_0}}}{{2R}}$
$\Rightarrow \dfrac{{{P_0}}}{{{V_0}}}\dfrac{V}{R} = \dfrac{{3{P_0}}}{{2R}}$
$\Rightarrow V = \dfrac{3}{2}{V_0}$

Now determine the maximum temperature of the gas during the expansion of the gas.

Rewrite equation (2) for maximum temperature ${T_{\max }}$ and substitute $\dfrac{{3{V_0}}}{2}$ for $V$ in it.
$\Rightarrow {T_{\max }} = - \dfrac{{{P_0}}}{{2{V_0}}}\dfrac{{{{\left( {\dfrac{{3{V_0}}}{2}} \right)}^2}}}{R} + \dfrac{{3{P_0}}}{2}\dfrac{{\dfrac{{3{V_0}}}{2}}}{R}$
$\Rightarrow {T_{\max }} = - \dfrac{{9{P_0}{V_0}}}{{8R}} + \dfrac{{9{P_0}{V_0}}}{{4R}}$
$\Rightarrow {T_{\max }} = \dfrac{{9{P_0}{V_0}}}{{8R}}$

Therefore, the maximum temperature is $\dfrac{{9{P_0}{V_0}}}{{8R}}$.

So, the correct answer is “Option C”.

Note:
The ideal gas equation is considered for one mole of gas. Hence, the resulting equation is the product of pressure of the gas and volume of the gas equal to product of the gas constant and the temperature of the gas in kelvin.